кинематика
Круговая трактриса
Я люблю задачки, в которых нужно искать траектории частиц или уравнения необычных линий. К сожалению, они не всегда решаются аналитически. Разберем задачу, у которой аналитическое решение существует.
Задача
По окружности небольшого радиуса едет трактор. К нему на жестком стержне прикреплен груз (например, прицеп). По какой траектории будет двигаться груз?
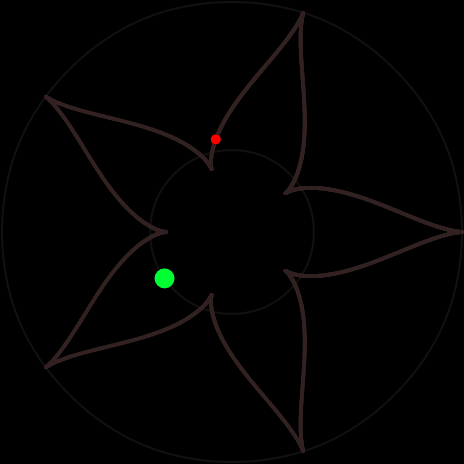
При движении трактора по прямой траектория груза известна — это трактриса. В нашем случае движение будет более сложным. Я сделал анимацию искомой траектории — круговой трактрисы. Посмотрите на эту красоту.
Решение
Будем считать трактор точкой, движущейся по окружности радиуса r, и обозначать на рисунках зеленым кружком. К нему с помощью стержня длины L прикреплен груз (красный кружок).
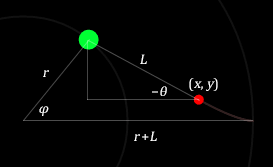
Из кинематических связей координаты груза определяются формулами
$$x=r\cos\varphi+L\cos\theta,\quad y=r\sin\varphi+L\sin\theta.$$
Еще одна кинематическая связь дает ограничение на скорость груза. По условию вектор скорости всегда направлен на трактор. Поэтому угол θ в прямоугольном треугольнике совпадает с точностью до знака с углом наклона касательной:
$${dy\over dx}=\text{tg\,}\theta.$$
Мы выразим θ через φ и получим уравнение траектории в параметрической форме. Введем новый параметр β = L/r, возьмем дифференциалы первых двух уравнений и подставим в последнее:
$$-{\cos\varphi\,d\varphi+\beta\cos\theta\,d\theta\over \sin\varphi\,d\varphi+\beta\sin\theta\,d\theta}=\text{tg\,}\theta.$$
Приведя к общему знаменателю и воспользовавшись основным тригонометрическим тождеством и формулой косинуса разности, получаем дифференциальное уравнение
$$\beta{d\theta\over d\varphi}+\cos(\theta-\varphi)=0.$$
Оно решается разделением переменных после замены θ = α + φ. Решение имеет разный вид в зависимости от параметра β:
$$\theta(\varphi)=\left\{\begin{array}{l}\varphi-2\,\text{arctg}\left[\sqrt{\dfrac{\beta+1}{\beta-1}}\,\text{tg}\left(\varphi\,\dfrac{\sqrt{\beta^2-1}}{2\beta}\right)\right],\quad\beta>1,\\\vphantom{\dfrac{1}{1}}\varphi-2\,\text{arctg}\,\varphi,\quad\beta=1,\\\varphi-2\,\text{arctg}\left[\sqrt{\dfrac{1+\beta}{1-\beta}}\,\text{th}\left(\varphi\,\dfrac{\sqrt{1-\beta^2}}{2\beta}\right)\right],\quad\beta<1.\end{array}\right.$$
Анализ решения
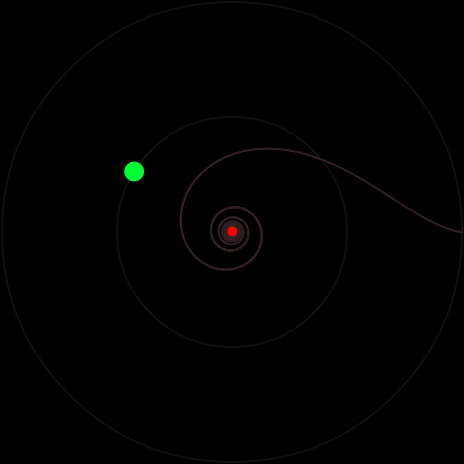
Если β < 1, движение непериодическое. Груз следует за трактором, асимпотически приближаясь к окружности. Интересный режим возникает при β = 1. Тогда груз неограниченно приближается к центру окружности:
Если β > 1, движение будет периодическим по звездообразной траектории:
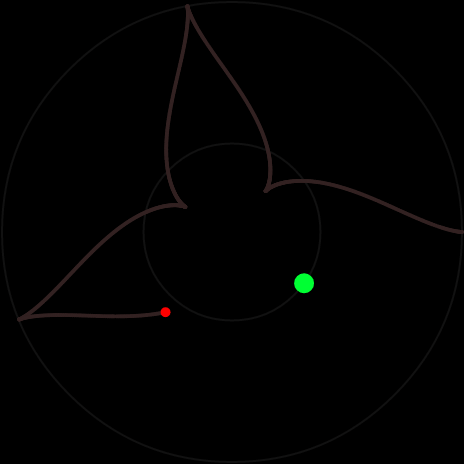
Чтобы найти угол между направлениями на соседние максимум и минимум, заметим, что груз находится дальше всего от центра, когда θ и φ совпадают, и ближе всего к центру, когда отличаются на π. В первом случае тангенс равен нулю, во втором — расходится. Возьмем направление на максимум θ = φ = 0 и направление на первый минимум φ = θ + π, определяющийся условием
$$(\pi+\theta)\,{\sqrt{\beta^2-1}\over 2\beta}={\pi\over 2}.$$
Угол между направлениями составляет
$$\theta=\pi\left({\beta\over\sqrt{\beta^2-1}}-1\right).$$
Если параметр удовлетворяет условию
$${1\over N}={\beta\over\sqrt{\beta^2-1}}-1,$$
то груз описывает замкнутую линию — N-конечную звезду. Вот пример для $$N=5,\beta=6/\sqrt{11}$$: