теория вероятностей

Задача о математическом ожидании количества случайных слагаемых

Недавно Майкл Пенн разбирал интересную задачу, которую я cформулирую так:

Сколько в среднем нужно взять случайных натуральных чисел, равномерно распределенных на отрезке от 1 до $$n$$, чтобы их сумма превысила $$n$$?

Конструкция в его решении выглядит достаточно искусственной и требует непростых рассуждений. Я предлагаю решить задачу «в лоб», без применения хитрых конструкций. Оказывается, это можно сделать, немного повозившись с преобразованием сумм.

Решение

Ясно, что одного числа $$a_1\in[1,n]$$ недостаточно, чтобы сумма $$a_1$$ превысила $$n$$. Два числа уже могут в сумме $$a_1+a_2$$ дать число, большее $$n$$. Если это произошло, испытание завершается. В противоположном случае нужно выбрать еще одно число и т. д.

Обозначим через $$P_n(k)$$ вероятность неуспеха — вероятность того, что сумма случайно выбранных $$k$$ чисел окажется не больше $$n$$:

$$P_n(k)=P\left(\sum\limits_{i=1}^{k}a_i\leq n\right).$$(1)

Cхему одного испытания можно представить в виде дерева, где добавление нового числа при неуспехе каждый раз порождает развилку:

$$ \tikzstyle{level 1}=[level distance=5cm] \tikzstyle{level 2}=[level distance=6cm] \tikzstyle{bag}=[fill=red!20] \tikzstyle{end}=[fill=green!20] \begin{tikzpicture}[grow=right, sloped,sibling distance = 15mm] \node[bag, label=above:{$P_n(1)=1$}] {$a_1\leq n$} child[edge from parent/.style={draw, -latex, line width=0.8mm, black!30}] { node[end] {$a_1+a_2>n$} edge from parent node[below,black] {$P_n(1)-P_n(2)$} } child[edge from parent/.style={draw, -latex, line width=3mm, black!30}] { node[bag] {$a_1+a_2\leq n$} child[edge from parent/.style={draw, -latex, line width=1.2mm, black!30}] { node[end] {$a_1+a_2+a_3>n$} edge from parent node[below,black] {$P_n(2)-P_n(3)$} } child[edge from parent/.style={draw, -latex, line width=1.8mm, black!30}] { node[bag, label=right:{...}] {$a_1+a_2+a_3\leq n$} edge from parent node[above,black] {$P_n(3)$} } edge from parent node[above,black] {$P_n(2)$} }; \end{tikzpicture} $$

Из нее мы видим, что вероятность того, что в одном испытании будет взято ровно $$k$$ чисел, равна $$P_n(k-1)-P_n(k)$$. Действительно, событие, противоположное (1), состоит в том, что сумма произвольного не превосходящего $$k$$ количества случайно взятых чисел будет больше $$n$$. Его вероятность есть $$1-P_n(k)$$. Аналогично, вероятность того, что сумма произвольного не превосходящего $$k-1$$ количества случайно взятых чисел будет больше $$n$$ есть $$1-P_n(k-1)$$. Разность этих величин как раз и дает $$P_n(k-1)-P_n(k)$$.

Тогда искомое среднее $$N$$ можно выразить как

$$\begin{align*}N&=2\left[P_n(1)-P_n(2)\right]+3\left[P_n(2)-P_n(3)\right]+\ldots+(n+1)\left[P_n(n)-P_n(n+1)\right]=\\ &=2+P_n(2)+P_n(3)+P_n(4)+\ldots+P_n(n).\end{align*}$$(2)

В этой сумме мы раскрыли скобки и сгруппировали промежуточные слагаемые. Ясно, что дерево вероятностей конечно, и последняя ненулевая вероятность $$P_n(n)=1/n^n$$ в нем соответствует случаю $$a_1=a_2=\ldots=a_n=1$$. Поэтому сумма в (2) заканчивается на нулевом слагаемом $$-(n+1)P_n(n+1)=0$$, тем самым кроме сгруппированных промежуточных слагаемых никаких слагаемых в конце в ней нет.

Начнем с вычисления $$P_n(2)$$. Пространство элементарных событий для двух натуральных чисел от 1 до $$n$$ можно представить матрицей $$n\times n$$, в которой неудачные исходы $$a_1+a_2\leq n$$ расположены под главной диагональю:

$$ \tikzstyle{bad}=[fill=red!10!white, minimum width=0.98cm, minimum height=0.98cm] \tikzstyle{good}=[fill=green!10!white, minimum width=0.98cm, minimum height=0.98cm] \begin{tikzpicture}[scale=1] \draw[step=1] (0,0) grid (5,5); \node[bad] at (0.5,0.5) {2}; \node[bad] at (1.5,0.5) {3}; \node[bad] at (0.5,1.5) {3}; \node[good] at (4.5,4.5) {$2n$}; \foreach \x in {0,...,4} { \node[good] at (0.5+\x, 4.5-\x) {$n$+1}; } \foreach \x in {0,...,3} { \node[good] at (1.5+\x, 4.5-\x) {$n$+2}; } \foreach \x in {0,...,2} { \node[good] at (2.5+\x, 4.5-\x) {}; } \foreach \x in {0,...,1} { \node[good] at (3.5+\x, 4.5-\x) {}; } \foreach \x in {0,...,3} { \node[bad] at (0.5+\x, 3.5-\x) {$n$}; } \foreach \x in {0,...,2} { \node[bad] at (0.5+\x, 2.5-\x) {}; } \draw[->] (0,-0.5) -- ++(5,0) node[pos=0.5,below] {$a_1$}; \draw[->] (-0.5,0) -- ++(0,5) node[pos=0.5,left] {$a_2$}; \end{tikzpicture} $$

Искомая вероятность $$P_n(2)$$ равна отношению количества красных квадратиков к общему количеству квадратиков. Вычисляя, получаем, что она связана с треугольными числами $$T_n=n(n+1)/2$$:

$$P_n(2)={1\over n^2}\sum\limits_{a_1+a_2\leq n}1={1\over n^2}\sum\limits_{a_1=1}^{n-1}n-a_1={1\over n^2}\cdot{(n-1)n\over 2}={T_{n-1}\over n^2}={C_n^2\over n^2}.$$

Перейдем к $$P_n(3)$$. Пространство элементарных событий для трех чисел можно представить себе как часть куба $$n\times n\times n$$, нарезанного на единичные кубики. Нас интересуют неудачные исходы $$a_1+a_2+a_3\leq n$$, которые соответствуют такой пирамидке:

$$ \usetikzlibrary {perspective} \colorlet{cube color}{blue!50!cyan} \begin{tikzpicture}[3d view={110}{25},scale=0.8, line join=round, line cap=round,every path/.style={cube color,thick}] \def\k{1.2} \def\n{2} \draw[black,thin,->] (0,0) -- ++(0,4.4) node[pos=0.9,above] {$a_1$}; \draw[black,thin,->] (0,0) -- ++(4.5,0) node[pos=0.9,left] {$a_2$}; \draw[black,thin,->] (0,0,0) -- ++(0,0,4.2) node[pos=0.9,left] {$a_3$}; \foreach \z in {0,...,\n} { \pgfmathsetmacro{\ymax}{\n-\z} \foreach \y in {0,...,\ymax} { \pgfmathsetmacro{\xmax}{\ymax-\y} \foreach \x in {0,...,\xmax} { \draw[fill=cube color!30] (\k*\x, \k*\y, \k*\z+1) -- ++(1, 0, 0) -- ++(0, 1, 0) -- ++(-1, 0, 0) -- cycle; \draw[fill=cube color!50] (1+\k*\x, \k*\y, \k*\z) -- ++(0, 0, 1) -- ++(0, 1, 0) -- ++(0, 0, -1) -- cycle; \draw[fill=cube color!70] (\k*\x, \k*\y+1, \k*\z) -- ++(1, 0, 0) -- ++(0, 0, 1) -- ++(-1, 0, 0) -- cycle; } } } \end{tikzpicture}$$

Здесь мы можем предположить, что вероятность $$P_n(3)$$ выражается через тетраэдральные числа $$\inlineTe_n=\sum_{k=1}^nT_n$$. Формально этот результат получается при вычислении суммы на множестве $$a_1+a_2+a_3\leq n$$ по слоям: сначала по слою $$a_1+a_2+a_3=n$$, потом по слою $$a_1+a_2+a_3=n-1$$ и т. д:

$$ \usetikzlibrary {perspective} \colorlet{cube color}{blue!50!cyan} \begin{tikzpicture}[3d view={110}{25},scale=0.8, line join=round, line cap=round,every path/.style={cube color,thick}] \def\k{1.2} \def\n{2} \foreach \z in {0,...,\n} { \pgfmathsetmacro{\ymax}{\n-\z} \foreach \y in {0,...,\ymax} { \pgfmathsetmacro{\xmax}{\ymax-\y} \foreach \x in {0,...,\xmax} { \pgfmathtruncatemacro{\layer}{\x + \y + \z} \ifnum \layer=2 \colorlet{cube color}{blue!50!cyan} \fi \ifnum \layer=1 \colorlet{cube color}{olive} \fi \ifnum \layer=0 \colorlet{cube color}{orange} \fi \draw[fill=cube color!30] (\k*\x, \k*\y, \k*\z+1) -- ++(1, 0, 0) -- ++(0, 1, 0) -- ++(-1, 0, 0) -- cycle; \draw[fill=cube color!50] (1+\k*\x, \k*\y, \k*\z) -- ++(0, 0, 1) -- ++(0, 1, 0) -- ++(0, 0, -1) -- cycle; \draw[fill=cube color!70] (\k*\x, \k*\y+1, \k*\z) -- ++(1, 0, 0) -- ++(0, 0, 1) -- ++(-1, 0, 0) -- cycle; \pgfmathsetmacro{\s}{5.5+5*(\n-\layer)} \pgfmathsetmacro{\p}{-1-2.5*(\n-\layer)} \pgfmathsetmacro{\t}{0.45} \draw[fill=cube color!30] (\k*\x+\p, \k*\y+\s, \k*\z+1+\t) -- ++(1, 0, 0) -- ++(0, 1, 0) -- ++(-1, 0, 0) -- cycle; \draw[fill=cube color!50] (1+\k*\x+\p, \k*\y+\s, \k*\z+\t) -- ++(0, 0, 1) -- ++(0, 1, 0) -- ++(0, 0, -1) -- cycle; \draw[fill=cube color!70] (\k*\x+\p, \k*\y+1+\s, \k*\z+\t) -- ++(1, 0, 0) -- ++(0, 0, 1) -- ++(-1, 0, 0) -- cycle; } } } \node[black] at (0,4,1.25) {$=$}; \node[black] at (0,10,2.25) {$+$}; \node[black] at (0,15.5,3.15) {$+$}; \end{tikzpicture}$$

$$\begin{align*} P_n(3)&={1\over n^3}\sum\limits_{a_1+a_2+a_3\leq n}1={1\over n^3}\left(\sum\limits_{a_1+a_2+a_3=n}1+\sum\limits_{a_1+a_2+a_3=n-1}1+\ldots\right)=\\ &={1\over n^3}\left(\sum\limits_{a_1+a_2\leq n-1}1+\sum\limits_{a_1+a_2\leq n-2}1+\ldots\right). \end{align*}$$

Каждая из сумм в скобках уже вычислена на предыдущем этапе. Действительно, количество элементов в слоях задается треугольными числами. Подставляем:

$$P_n(3)={1\over n^3}(T_{n-2}+T_{n-3}+\ldots)={Te_{n-2}\over n^3}={C_n^3\over n^3}.$$

Идея с послойным вычислением суммы без каких-либо изменений обобщается на случай произвольного количества чисел $$k$$. Вероятность $$P_n(k)$$ будет выражаться через гипертетраэдральные числа:

$$P_n(k)={C_n^k\over n^k}.$$(3)

Подставим в (2):

$$N=2+{C_n^2\over n^2}+{C_n^3\over n^3}+{C_n^4\over n^4}+\ldots+{C_n^n\over n^n}.$$

А это есть не что иное, как разложение $$(1+1/n)^n$$ через бином Ньютона. Ответ:

$$N=\left(1+{1\over n}\right)^n.$$

Обсуждение

В пределе неограниченно больших $$n$$ ожидаемое количество слагаемых стремится к $$e$$. Да и сама задача в этом пределе переходит в известную задачу о математическом ожидании количества случайных величин, равномерно распределенных на интервале от 0 до 1, таких чтобы их сумма превзошла 1. О том, что это математическое ожидание равно $$e$$, я узнал из книги Мартина Гарднера «Математические досуги»:

Идея рассуждений в непрерывном случае аналогична нашему решению, а детали вычислений оказываются проще. Суммы заменяются на интегралы от многочленов, которые без проблем вычисляются и дают меру симплекса, построенного на единичных отрезках на осях координат: $$P(k)=1/k!$$. Сумма в (2) становится бесконечной и превращается в известный ряд для числа $$e=1+1/1!+1/2!+\ldots$$

В дискретном случае приходится заниматься конечными суммами, которые сводятся к треугольным числам и их обобщениям. Надо сказать, что для решения никакие их свойства не использовались. Явный вид $$P_n(k)$$ можно было получить для нескольких начальных $$k$$ и затем по индукции доказать общий вид (3). Либо можно воспользоваться свойствами чисел, стоящих на местах с номером $$k$$ в треугольнике Паскаля:

$$ \makeatletter \newcommand\binomialcoefficient[2]{ % Store values \c@pgf@counta=#1% n \c@pgf@countb=#2% k % % Take advantage of symmetry if k > n - k \c@pgf@countc=\c@pgf@counta% \advance\c@pgf@countc by-\c@pgf@countb% \ifnum\c@pgf@countb>\c@pgf@countc% \c@pgf@countb=\c@pgf@countc% \fi% % % Recursively compute the coefficients \c@pgf@countc=1% will hold the result \c@pgf@countd=0% counter \pgfmathloop% c -> c*(n-i)/(i+1) for i=0,...,k-1 \ifnum\c@pgf@countd<\c@pgf@countb% \multiply\c@pgf@countc by\c@pgf@counta% \advance\c@pgf@counta by-1% \advance\c@pgf@countd by1% \divide\c@pgf@countc by\c@pgf@countd% \repeatpgfmathloop% \the\c@pgf@countc% } \makeatother \begin{tikzpicture}[scale=0.8] \node[red, right] at (0.9,-0.5) {Натуральные числа}; \node[orange, right] at (1.4,-1.5) {Треугольные числа}; \node[olive, right] at (1.9,-2.5) {Тетраэдральные числа}; \node[right] at (2.4,-3.5) {...}; \foreach \n in {0,...,7} { \foreach \k in {0,...,\n} { \ifnum \k=0 \node[black] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=1 \node[red,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=2 \node[orange,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=3 \node[olive,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=4 \node[green!70!black,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=5 \node[blue,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=6 \node[magenta,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=7 \node[purple,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi } } \end{tikzpicture}$$

Задача коллекционера

Представьте, что вы кидаете игральный кубик, и выпадает число от 1 до 6. Сколько раз в среднем нужно бросить кубик до того момента, как каждое число выпадет хотя бы один раз? Ясно, что число попыток не должно быть меньше 6. Но если при этом попадались одинаковые числа, потребуется больше бросков. Сколько именно?

Это одна из возможных формулировок задачи коллекционера. Под таким названием (Coupon Collector’s Problem) она встречается в англоязычной литературе, а в русскоязычной практически не упоминается (я нашел одну публикацию в «Математическом просвещении»). Давайте исправим несправедливость и разберем эту весьма интересную задачу.

Современному читателю проще прочувствовать смысл этой задачи на примере киндер-сюрприза: сколько нужно купить шоколадных яиц, внутри которых находится одна из $$N$$ машинок, чтобы собрать полную коллекцию?

Стандартное решение

Обозначим через $$T$$ искомое количество попыток сбора $$N$$ элементов коллекции. Оно состоит из суммы числа попыток $$t_i$$ получить элемент $$i$$, когда уже собрано $$i-1$$ элементов: $$T=t_1 + \cdots + t_N$$.

Вероятность найти новый $$i$$-й элемент коллекции, когда уже собрано $$i-1$$ элементов и осталось собрать $$N-i+1$$, равна

$$P(i)={N-i+1\over N}.$$(1)

То есть $$t_i$$ — случайная величина с геометрическим распределением и математическим ожиданием

$$\operatorname{E}(t_i)=\frac{1}{P(i)}=\frac{N}{N-i+1}.$$(2)

С учетом линейности математического ожидания

$$\begin{align*} \operatorname{E}(T) & {}= \operatorname{E}(t_1 + t_2 + \cdots + t_N)=\\ &=\operatorname{E}(t_1) + \operatorname{E}(t_2) + \cdots + \operatorname{E}(t_N)=\\ &=\frac{1}{P(1)} + \frac{1}{P(2)} + \cdots + \frac{1}{P(N)}=\\ &=\frac{N}{N} + \frac{N}{N-1} + \cdots + \frac{N}{1}=\\ &=N \cdot \left(\frac{1}{1} + \frac{1}{2} + \cdots + \frac{1}{N}\right)=\\ &=N H_N. \end{align*}$$

Здесь $$H_N$$ — частичные суммы гармонического ряда, асимптотика которых выражается через логарифм:

$$\operatorname{E}(T)=NH_{N}=N\ln N+\gamma N+{1\over 2}+O\left({1\over N}\right).$$(3)

Альтернативное решение

Решение выше получилось достаточно простым благодаря тому, что вероятность получения нового элемента коллекции (1) не зависит от истории, то есть от самих величин $$t_i$$. Однако такая зависимость может появиться в более сложном случае. Скажем, если коллекционер обменивается с другими коллекционерами, то чем больше у него накопилось дублей в коллекции, тем больше вероятность получить новый элемент через обмен. В этом примере формула (1) усложняется, а (2) вообще не работает.

В общем случае вероятность появления нового элемента может явно зависеть от номера шага $$t$$. Через $$P_t(n)$$ мы обозначим вероятность того, что после $$t$$ шагов мы собрали $$n$$ элементов коллекции. Я проведу рассуждения в условиях исходной задачи, а вы при необходимости можете их обобщить.

Если после выполнения $$t$$ шагов мы собрали $$n$$ элементов, это значит, что на предыдущем шаге количество элементов могло быть либо $$n-1$$, либо $$n$$. В первом случае мы получаем новый элемент с вероятностью, определяемой формулой (1), во втором случае противоположной вероятностью:

$$P_t(n)=\left(1-{n-1\over N}\right)P_{t-1}(n-1)+{n\over N}P_{t-1}(n).$$(4)

Это уравнение вместе с граничными условиями содержит в себе всю информацию из условия задачи, поэтому все остальные рассуждения будут чисто техническими.

О каких граничных условиях идет речь? Ясно, что $$P_0(0)=1$$, $$P_0(n)=0, 0<n\leq N$$ (в начале никакой коллекции нет). Кроме того, на первом шаге мы гарантированно получим один элемент, поэтому $$P_t(0)=0, t>0$$.

Перепишем для удобства (4) в другом виде после подстановки $$n=N-m$$:

$$P_t(N-m)={m+1\over N}P_{t-1}\left(N-(m+1)\right)+{N-m\over N}P_{t-1}(N-m)$$(4a)

Заметим еще, что на каждом шаге должна сохраняться нормировка вероятности — в коллекции точно должно быть хоть сколько-то элементов:

$$\sum_{n=0}^N P_t(n)=1.$$(5)

Нарушение условия нормировки сразу укажет на ошибку в построении математической модели. Давайте проверим, что в (4) подобных ошибок нет:

$$\begin{align*} \sum_{n=0}^N P_t(n)&=P_t(0)+\sum_{n=1}^N \left[\left(1-{n-1\over N}\right)P_{t-1}(n-1)+{n\over N}P_{t-1}(n)\right]=\\ &=\sum_{n=0}^{N-1} \left(1-{n\over N}\right)P_{t-1}(n)+\sum_{n=1}^N {n\over N}P_{t-1}(n)=\\ &=\sum_{n=0}^{N-1}P_{t-1}(n)-{0\over N}P_{t-1}(0)+{N\over N}P_{t-1}(N)=\\ &=\sum_{n=0}^{N}P_{t-1}(n). \end{align*}$$

Мы опустили нулевое слагаемое $$P_t(0)$$ из граничных условий, а также перенумеровали слагаемые в одной из сумм. По индукции видно, что нормировка сохраняется на каждом шаге.

В задаче нам нужно усреднить число попыток $$t$$ до окончания сбора коллекции:

$$\operatorname{E}(T)=\sum\limits_tt\left(P_t(N)-P_{t-1}(N)\right).$$

Чтобы получить вероятность окончания сбора коллекции именно на шаге $$t$$, я вычел из вероятности собрать $$N$$ элементов на шаге $$t$$ вероятность собрать $$N$$ элементов на шаге $$t-1$$ (вычитается вероятность того, что на предыдущем шаге коллекция уже собрана).

Из (4а) при $$m=0$$:

$$P_t(N)={1\over N}P_{t-1}\left(N-1\right)+P_{t-1}(N).$$

Отсюда

$$\operatorname{E}(T)={1\over N}\sum\limits_ttP_{t-1}(N-1).$$(6)

Здесь мы видим другое представление вероятности окончания сбора коллекции: вероятность сбора последнего элемента $$1/N$$ умножается на вероятность наличия $$N-1$$ элементов на предыдущем шаге.

Идея дальнейших вычислений в том, чтобы пользуясь равенством (4а) и дальше понижать аргумент в (6) от $$N-1$$ до 0. Тогда в сумме останется только один ненулевой элемент, соответствующий $$P_0(0)=1$$. Вы можете проделать несколько подстановок (4а) вручную и увидеть закономерность. Я же сразу сформулирую ее в виде утверждения, связывающего $$\operatorname{E}(T)$$ и $$P_{t}(N-m)$$:

Утверждение. Существуют такие числа $$A_m$$ и $$B_m$$, что при любых натуральных $$N$$ и $$m\in [1,N]$$ выполняется равенство

$$\operatorname{E}(T)={m\over N}\sum\limits_ttP_{t-m}(N-m)+A_mN-B_m.$$(7)

Доказательство по индукции. Если $$m=1$$, то из (6) гипотеза верна при $$A_1=B_1=0$$. Пусть она верна для $$m>1$$. Тогда из (4а)

$$\begin{align*}\operatorname{E}(T)&={m\over N}\sum_tt\left[{m+1\over N}P_{t-m-1}\left(N-(m+1)\right)+{N-m\over N}P_{t-m-1}(N-m)\right]+A_mN-B_m=\\ &={m\over N}{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+{N-m\over N}\underbrace{{m\over N}\sum_ttP_{t-m-1}(N-m)}_{S_1}+A_mN-B_m.\end{align*}$$

Сумма в первом слагаемом похожа на нужную сумму из (7) для $$m$$, увеличенного на 1. Пока отдельно вычислим оставшуюся сумму:

$$\begin{align*}S_1&={m\over N}\sum\limits_ttP_{t-m-1}(N-m)=\\ &={m\over N}\sum_{t+1}(t+1)P_{t-m}(N-m)=\\ &={m\over N}\sum_ttP_{t-m}(N-m)+{m\over N}\sum_tP_{t-m}(N-m)=\\ &=\operatorname{E}(T)-A_mN+B_m+\underbrace{{m\over N}\sum_tP_t(N-m)}_{S_2}.\end{align*}$$

Здесь мы дважды воспользовались изменением индекса суммирования. Так как суммирование идет по всем возможным $$t$$, мы можем спокойно менять индексы. Лишних или отсутствующих слагаемых не будет, так как вероятности зануляются, когда число шагов меньше размера коллекции: $$P_t(n)=0, t<n$$.

Просуммируем теперь (4a) по всем $$t$$:

$$\begin{align*}\sum_tP_t(N-m)&=\sum_t{m+1\over N}P_{t-1}\left(N-(m+1)\right)+\sum_t{N-m\over N}P_{t-1}(N-m)=\\ &={m+1\over N}\sum_tP_t\left(N-(m+1)\right)+{N-m\over N}\sum_tP_t(N-m), \end{align*}$$

откуда

$${m\over N}\sum_tP_t(N-m)=\sum_t{m+1\over N}P_t\left(N-(m+1)\right).$$

Таким образом, по индукции $$\inlineS_2={m\over N}\sum_tP_t(N-m)$$ не зависит от $$m$$ и равно 1, так как при $$m=N$$ переходит в $$P_0(0)+P_1(0)+P_2(0)+\ldots=1+0+0+\ldots=1$$. Возвращаемся к $$\operatorname{E}(T)$$:

$$\begin{align*}\operatorname{E}(T)&={m\over N}{m+1\over N}\sum\limits_ttP_{t-m-1}\left(N-(m+1)\right)+\\ &+{N-m\over N}(\operatorname{E}(T)-A_mN+B_m+1)+A_mN-B_m,\\ N\operatorname{E}(T)&=m{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+\\&+\operatorname{E}(T)N-A_mN^2+B_mN+N-m\operatorname{E}(T)+mA_mN-mB_m-m+A_mN^2-B_mN,\\ m\operatorname{E}(T)&=m{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+N+mA_mN-mB_m-m,\\ \operatorname{E}(T)&={m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+(A_m+{1/m})N-(B_m+1).\end{align*}$$

По форме это совпадает с (7) при условии

$$A_{m+1}=A_m+{1\over m},\quad B_{m+1}=B_m+1.$$

С учетом начальных условий $$A_1=B_1=0$$ получаем явные выражения коэффициентов: $$A_m=1+1/2+\ldots+1/(m-1)=H_{m-1}$$ — частичные суммы гармонического ряда, $$B_m=m-1$$. $$\square$$

Подставим теперь $$m=N$$ в (7). Тогда

$$\omeratorname{E}(T)=\sum_ttP_{t-N}(0)+H_{N-1}N-N+1=H_{N-1}N+1=N\left(H_{N-1}+{1\over N}\right)=NH_N,$$

что совпадает с ответом стандартного решения.

Вывод

Мы решили задачу коллекционера, записав уравнение эволюции распределения вероятности (4). Это уравнение можно рассматривать как дискретный вариант уравнения, описывающего поток вероятности.

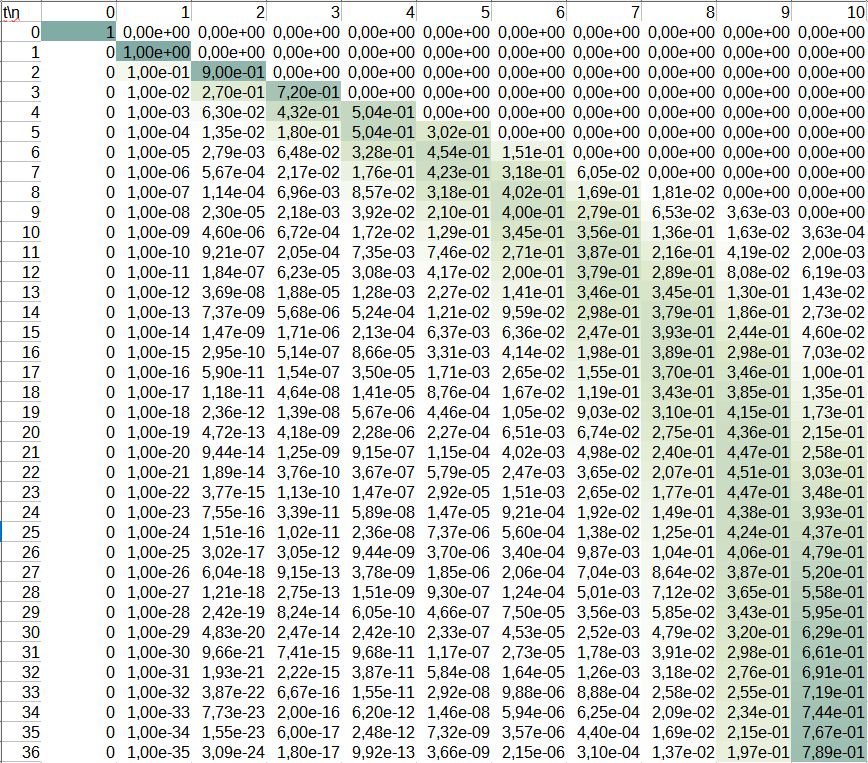
Такой подход универсален для задач подобного типа, потому что позволяет их решать не только аналитически, но и численно. Например, в нашем случае эволюцию распределения вероятности можно рассчитать на основе уравнения (4) даже в Excel. На скриншоте видно, как распределение вероятности со временем смещается от меньших $$n$$ к большим для $$N=10$$.

Задача о взвешенном выборе и случайной величине: единственность решения

В прошлый раз мы решали задачу о взвешенной сортировке и показали, что существует функция $$f_w(x)$$, такая что максимальное значение этой функции $$\inline\max_{i=1,2,...n}\left\{f_{w_i}(x_i)\right\}$$ будет достигнуто на k-той паре $$(w_k, x_k)$$ с вероятностью, пропорциональной $$w_k$$, где $$x_i$$ — значение случайной величины, равномерно распределенной на единичном отрезке $$[0, 1]$$.

Мы потребовали непрерывности и монотонности функции $$f_w(x)$$ по $$x$$, а также зафиксировали значения на концах отрезка: $$f_w(0) = a, f_w(1) = b$$. В этих предположениях показали, что функция должна удовлетворять условию

$$ \int\limits_0^1dx_1\,f^{-1}_{w_2}\left(f_{w_1}(x_1)\right)\cdot f^{-1}_{w_3}\left(f_{w_1}(x_1)\right)\cdot\ldots\cdot f^{-1}_{w_n}\left(f_{w_1}(x_1)\right) ={w_1\over w_1+w_2+w_3+\ldots+w_n} $$(1)

для любых наборов значений $$w_i>0$$. Мы нашли целый класс подходящих под это условие функций:

$$f_w(x)=h(x^{1/w}),$$(2)

где $$h(y)$$ — любая строго монотонная функция.

Теперь докажем, что других решений у этой задачи не существует.

Теорема о единственности. Пусть для каждого значения $$w>0$$ функция $$f_w(x)$$ непрерывна и строго монотонна по $$x$$ на отрезке $$[0,1]$$, принимает на концах отрезка фиксированные значения $$f_w(0) = a, f_w(1) = b$$ и удовлетворяет (1). Тогда найдется такая строго монотонная функция $$h(y)$$, для которой выполняется тождество (2).

Доказательство будет конструктивным: мы построим конкретный пример $$h(y)$$ на основе вида функции $$f_w(x)$$.

Лемма 1. Обратная функция $$f^{-1}_w(s)$$ при каждом фиксированном значении аргумента $$s\in[a,b]$$ непрерывна по параметру $$w$$ на всем допустимом множестве значений этого параметра $$w>0$$.

Доказательство от противного. Пусть существует точка $$w_2$$, в которой $$f^{-1}_w(s)$$ не является непрерывной. Это значит, что

$$\exists\varepsilon>0\ \forall\delta_1>0\ \exists s_1\in[a,b]\ \exists w_3:|w_2-w_3|<\delta_1,\left|f^{-1}_{w_2}(s_1)-f^{-1}_{w_3}(s_1)\right|>\varepsilon.$$(3)

Так как функция $$f^{-1}_w(s)$$ непрерывна по $$s$$ на отрезке $$[a,b]$$, она равномерно непрерывна на нем в силу теоремы Кантора — Гейне. Из равномерной непрерывности следует, что $$|f^{-1}_{w_2}(s)-f^{-1}_{w_3}(s)|>\varepsilon/2$$ в некоторой $$\delta_2$$-окрестности точки $$s_1$$, причем $$\delta_2$$ зависит только от $$\varepsilon$$, не от $$s_1$$. (Иными словами, разрыв по $$w$$ будет наблюдаться не только в одной точке $$s_1$$, но и в ее окрестности.)

Аналогично функция $$f_w(x)$$ непрерывна и равномерно непрерывна на отрезке $$[0,1]$$. По $$\delta_2$$-окрестности точки $$s_1$$ можно найти $$\delta_3$$-окрестность точки $$x_1=f^{-1}_{w_1}(s_1)$$, для каждого $$x$$ из которой $$\left|f^{-1}_{w_2}(f_{w_1}(x))-f^{-1}_{w_3}(f_{w_1}(x))\right|>\varepsilon/2$$ (значение $$w_1$$ выбирается произвольно и фиксируется для следующих рассуждений).

Это значит, что следующий интеграл от квадрата разности функций в соседних точках $$w_2$$ и $$w_3$$ ограничен снизу ненулевой величиной, не зависящей от $$\delta_1$$:

$$\int\limits_a^bdx\left[f^{-1}_{w_2}(f_{w_1}(x))- f^{-1}_{w_3}(f_{w_1}(x))\right]^2>{\delta_3\varepsilon^2\over 4}$$

Теперь непосредственно вычислим интеграл, раскрыв скобки и воспользовавшись условием (1):

$$ \begin{align*} &\int\limits_a^bdx\left[f^{-1}_{w_2}(f_{w_1}(x))- f^{-1}_{w_3}(f_{w_1}(x))\right]^2=\\ =&\!\int\limits_a^b\!dx\left[f^{-1}_{w_2}(f_{w_1}(x))\right]^2-2\!\int\limits_a^b\!dx\,f^{-1}_{w_2}(f_{w_1}(x))\, f^{-1}_{w_3}(f_{w_1}(x))+\!\int\limits_a^b\!dx\left[ f^{-1}_{w_3}(f_{w_1}(x))\right]^2=\\ =&{w_1\over w_1+2w_2}-2{w_1\over w_1+w_2+w_3}+{w_1\over w_1+2w_3}=\\ =&{2w_1\over(w_1+2w_2)(w_1+2w_3)(w_1+w_2+w_3)}(w_2-w_3)^2=\\ =&{2w_1\over(w_1+2w_2)(w_1+2w_2-2(w_2-w_3))(w_1+2w_2-(w_2-w_3))}(w_2-w_3)^2. \end{align*} $$

Оценка этого выражения снизу дает неравенство:

$${2w_1(w_2-w_3)^2\over(w_1+2w_2)(w_1+2w_2-2(w_2-w_3))(w_1+2w_2-(w_2-w_3))}>{\delta_3\varepsilon^2\over 4}.$$

Но согласно отрицанию определения непрерывности (3) $$\delta_1$$ можно выбрать сколь угодно малым, при этом $$\varepsilon$$, $$\delta_3$$ и $$w_1$$ зависят только от выбора $$w_2$$ и остаются фиксированными. Так как $$|w_2-w_3|<\delta_1$$, выбором $$\delta_1$$ также можно сделать левую часть неравенства сколь угодно малой при фиксированной правой. Противоречие. $$\square$$

Лемма 2. Для любых значений $$k,m\in\mathbb{N}$$, $$w>0$$, $$s\in[a,b]$$ выполняется равенство

$$\left[f^{-1}_{w/k}(s)\right]^k=\left[f^{-1}_{w/m}(s)\right]^m.$$

Доказательство. Введем в (1) новую переменную $$s=f_{w_1}(x_1)$$:

$$ \int\limits_a^bds\ {\partial f^{-1}_{w_1}(s)\over\partial s}\ f^{-1}_{w_2}(s)\cdot f^{-1}_{w_3}(s)\cdot\ldots\cdot f^{-1}_{w_n}(s) ={w_1\over w_1+w_2+w_3+\ldots+w_n}. $$

Разделим набор весов $$w_2$$, $$w_3$$, … $$w_n$$ на две группы количеством $$k$$ и $$m$$, в каждой из которых веса совпадают и равны $$w/k$$ и $$w/m$$ соответственно. Тогда:

$$ \int\limits_a^bds\ {\partial f^{-1}_{w_1}(s)\over\partial s}\ \left[f^{-1}_{w/k}(s)\right]^k \left[f^{-1}_{w/m}(s)\right]^m ={w_1\over w_1+2w}\quad\forall k,m\in\mathbb{N}. $$

Последний интеграл можно интерпретировать как скалярное произведение функций $$[f^{-1}_{w/k}(s)]^k$$ и $$[f^{-1}_{w/m}(s)]^m$$ в пространстве с положительной в силу монотонности $$f^{-1}_{w_1}$$ метрикой $$\partial f^{-1}_{w_1}(s)/\partial s$$. По неравенству Коши — Буняковского скалярное произведение не превосходит произведения норм, и равенство достигается при коллинеарности сомножителей. Из последнего уравнения видно, что скалярное произведение совпадает с квадратом нормы каждого элемента. Поэтому в нашем случае имеет место равенство. Действительно, вычислим норму от квадрата разности функций:

$$ \begin{align*} &\int\limits_a^bds\ {\partial f^{-1}_{w_1}(s)\over\partial s}\ \left\{\left[f^{-1}_{w/k}(s)\right]^k- \left[f^{-1}_{w/m}(s)\right]^m\right\}^2=\\ =&\int\limits_a^bds\ {\partial f^{-1}_{w_1}(s)\over\partial s}\ \left\{\left[f^{-1}_{w/k}(s)\right]^{2k} -2\left[f^{-1}_{w/k}(s)\right]^k\left[f^{-1}_{w/m}(s)\right]^m +\left[f^{-1}_{w/m}(s)\right]^{2m}\right\}=0. \end{align*} $$

Если предполагать противное — непрерывные функции не совпадают хотя бы в одной точке — интеграл от квадрата их разности не может быть нулевым. Противоречие.

Несмотря на присутствие в выражениях производной $$\partial f^{-1}_{w_1}(s)/\partial s$$, дифференцируемость по $$s$$ в этом доказательстве не требуется. Замена переменной $$x_1$$ на $$s$$ была проведена для удобства и наглядности. Аналогичные рассуждения имеют место и без замены переменных. $$\square$$

Следствие 1. Для любых значений $$r\in\mathbb{Q}_+$$, $$w>0$$, $$s\in[a,b]$$ выполняется равенство

$$f^{-1}_w(s)=\left[f^{-1}_{w/r}(s)\right]^r.$$

Доказательство. Представим положительное рациональное число $$r=m/k$$ как отношение натуральных чисел. В утверждении леммы 2 выполним замену $$w\to wk$$ и возведем обе части в степень $$1/k$$:

$$f^{-1}_w(s)=\left[f^{-1}_{wk/m}(s)\right]^{m/k}=\left[f^{-1}_{w/r}(s)\right]^r.\ \square$$

Следствие 2. Для любых значений $$p\in\mathbb{R}_+$$, $$w>0$$, $$s\in[a,b]$$ выполняется равенство

$$f^{-1}_w(s)=\left[f^{-1}_{w/p}(s)\right]^p.$$

Доказательство. Рассмотрим выражение $$[f^{-1}_{w/p}(s)]^p$$ как функцию от $$p$$. По следствию 1 в рациональных точках $$p$$ ее значение равно $$f^{-1}_w(s)$$. По лемме 1 функция непрерывна по параметру. Поэтому ее значение в иррациональных точках $$p$$ также равно $$f^{-1}_w(s)$$. $$\square$$

Доказательство теоремы. Из следствия 2 для любых $$p>0$$ выполняется равенство $$f_w(x)=f_{w/p}(x^{1/p})$$. Пусть $$p=w$$. Тогда

$$f_w(x)=f_1(x^{1/w})=h(x^{1/w}),$$

где $$h(y)\equiv f_1(y)$$ — строго монотонная функция. $$\square$$

Задача о взвешенном выборе и случайной величине

Условие

Пусть заданы n положительных чисел $$w_1$$, $$w_2$$, … $$w_n$$. Для каждого из них выберем значение $$x_i$$ случайной величины, равномерно распределенной на единичном интервале (0, 1). Существует ли функция $$f_w(x)$$, такая что максимальное значение этой функции $$\inline\max_{i=1,2,...n}\left\{f_{w_i}(x_i)\right\}$$ достигается на k-той выбранной паре $$(w_k, x_k)$$ с вероятностью, пропорциональной $$w_k$$?

Мотивация

Задача возникла из следующей программистской проблемы. Пусть в базе данных есть таблица с колонкой весов w. Нужно выбрать из этой таблицы случайную строку с вероятностью, пропорциональной значению веса w.

Можно было бы провести одно испытание, выбрав значение случайной величины $$x$$, и взять среди сумм $$w_1_$$, $$w_1 + w_2$$, $$w_1 + w_2 + w_3$$, … первую, превосходящую $$x(w_1 + w_2 + ... + w_n)$$. Но такой перебор сделать сложнее в синтаксисе SQL. Проще отсортировать таблицу по некоторой функции от веса и случайного числа:

SELECT * FROM table ORDER BY f(w, random()) DESC LIMIT 1

Какую функцию нужно применить к весу и случайному числу, чтобы значение этой функции на некоторой строке оказалось наибольшим с вероятностью, пропорциональной весу?

Решение

Допустим, что функция $$f_w(x)$$ существует. Пусть в первом выборе случайная величина приняла значение $$x_1$$. Вычислим, с какой вероятностью значение $$f_{w_1}(x_1)$$ будет наибольшим. Нам нужно взять меру множества значений $$x_i$$, на котором выполняется система неравенств:

$$ \begin{equation*} \begin{cases} f_{w_1}(x_1) > f_{w_2}(x_2),\\ f_{w_1}(x_1) > f_{w_3}(x_3),\\ \cdots \end{cases} \end{equation*} $$(1)

Предполагаем, что $$f_w(x)$$ непрерывна и монотонно возрастает по $$x$$. Тогда существует обратная функция $$f^{-1}_w(y)$$. Чтобы упростить рассмотрение на границах, предположим, что $$f_w(x)$$ принимает одинаковые значения на концах отрезка для всех значений параметра:

$$ f_w(0) = a,\quad f_w(1) = b. $$(2)

Тогда решением системы (1) будет множество

$$0<x_i<f^{-1}_{w_i}\left(f_{w_1}(x_1)\right),\quad i>1.$$

Меру этого множества нужно проинтегрировать по всем значениям $$x_1$$, чтобы вычислить вероятность получения максимального значения в первом выборе. С другой стороны, эта вероятность нормирована на 1 и по условию пропорциональна $$w_1$$. Выводим следующее ограничение на функцию $$f_w(x)$$ для произвольных значений $$w_i$$:

$$ \int\limits_0^1dx_1\,f^{-1}_{w_2}\left(f_{w_1}(x_1)\right)\cdot f^{-1}_{w_3}\left(f_{w_1}(x_1)\right)\cdot\ldots\cdot f^{-1}_{w_n}\left(f_{w_1}(x_1)\right) ={w_1\over w_1+w_2+w_3+\ldots+w_n}. $$(3)

Воспользуемся некоторыми эвристическими соображениями, которые позволяют угадать вид нашей функции. В интеграле можно перейти к новой переменной $$s=f_{w_1}(x_1)$$. Тогда подынтегральное выражение есть произведение величин $$f^{-1}_{w_2}(s)\cdot f^{-1}_{w_3}(s)\cdot\ldots\cdot f^{-1}_{w_n}(s)$$, а соответствующие веса в правой части входят только в виде суммы $$w_2+w_3+\ldots+w_n$$. Логично предположить, что обратная функция обладает показательным свойством по параметру:

$$f^{-1}_{w_2}(s)\cdot f^{-1}_{w_3}(s)\cdot\ldots\cdot f^{-1}_{w_n}(s) =f^{-1}_{w_2+w_3+\ldots+w_n}(s).$$(4)

Если обратная функция $$f^{-1}_w(y)$$ еще и непрерывна по этому параметру $$w$$, она имеет следующий вид: $$x=f^{-1}_w(y)=(g(y))^w$$, где $$g(y)$$ — некоторая новая монотонно возрастающая непрерывная функция. Отсюда следует, что прямая функция $$y=f_w(x)=g^{-1}(x^{1/w})$$.

Подставим полученный вид функций в интеграл из (3):

$$ \begin{align*} P_1&=\int\limits_0^1dx_1\,\left(g\left(g^{-1}(x_1^{1/w_1})\right)\right)^{w_2}\cdot \left(g\left(g^{-1}(x_1^{1/w_1})\right)\right)^{w_3}\cdot\ldots=\\ &=\int\limits_0^1dx_1\,\left(x_1^{1/w_1}\right)^{w_2+w_3+\ldots}= {1\over 1 +{w_2+w_3+\ldots\over w_1}}x_1^{1 +{w_2+w_3+\ldots\over w_1}}\Biggr|_0^1= {w_1\over w_1+w_2+\ldots+w_n}. \end{align*} $$

Таким образом, подстановка $$f_w(x)=g^{-1}(x^{1/w})$$ обращает уравнение (3) в тождество.

Вывод

Функция $$f_w(x)=x^{1/w}$$, а также ее композиция с любой монотонной функцией подходят для выбора из вариантов с заданными весами с помощью описанного в условии способа.

Обсудим единственность этого решения. Помимо естественного требования непрерывности и монотонности, мы наложили дополнительные ограничения (2) и (4). В этих предположениях решение единственно. В следующий раз мы рассмотрим вопрос единственности подробнее, а именно, появляются ли другие решения, если не требовать выполнения (2) и (4), а также можно ли вывести (2) и (4) непосредственно из условия или из более сильных ограничений на искомую функцию вроде дифференцируемости.