Гравитация в пространстве (2+1)
Мы рассмотрим некоторые особенности гравитации в трехмерном
Тензор Римана в (2+1)
Как известно, тензор Римана обладает следующими симметриями:
$$R_{abcd}=R_{cdab},\quad R_{abcd}=-R_{bacd}=-R_{abdc},$$
где каждый индекс пробегает значения 0, 1, 2. Непосредственным перебором легко проверить, что у тензора Римана остается 6 независимых ненулевых компонент: R0101, R0112, R0120, R1212, R1220, R2020. Число независимых компонент тензора Риччи тоже 6. Оказывается, в трехмерном
$$R_{abcd}=g_{ac}Q_{bd} + g_{bd}Q_{ac}-g_{ad}Q_{bc}-g_{bc}Q_{ad},$$(1)
где Qab ≡ Rab − ¼gabR, R ≡ Raa.
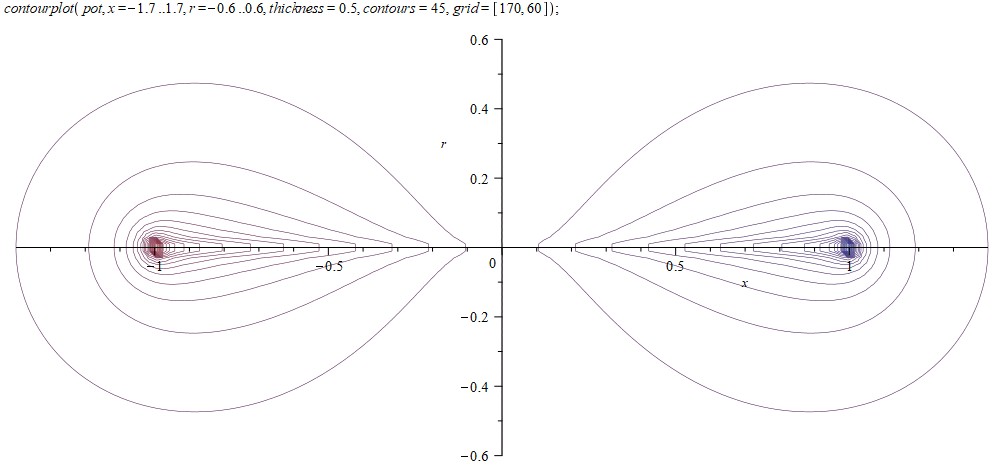
Точечная масса
Вычислим статическую
$$R_{ab} -{R \over 2} g_{ab} = {8 \pi G \over c^4} T_{ab}.$$
Взяв след обеих частей, получаем
$$R = -{16 \pi G \over c^4} T.$$(2)
В пустом пространстве вокруг тела Tab ≡ 0, следовательно, из (2), уравнения Эйнштейна и (1) получаем R ≡ 0, Rab ≡ 0, Rabcd ≡ 0. Таким образом, пустое пространство (2+1) должно быть локально плоским. Это, в частности, означает, что в рассматриваемом случае нет гравитационных волн.
Метрика такого пространства с учетом симметрий имеет следующий вид:
$$ds^2=-c^2dt^2+d\rho^2+\alpha^2\rho^2d\varphi^2,$$
где $$\alpha^2$$ — некоторая константа, а φ меняется от 0 до 2π. Введем новую угловую координату φ′ = αφ. Константа α и будет определять глобальные гравитационные эффекты. Заглядывая вперед, скажем, что α < 1. Таким образом, длина окружности, охватывающей точечную массу, будет меньше, чем 2πR.
Время входит в интервал с постоянным коэффициентом и не смешивается с другими координатами, поэтому скаляр кривизны R определяется только пространственной частью метрики.
Конический дефект
Двумерное пространство, описываемое такой метрикой, соответствует конической поверхности. В каждой точке поверхности, за исключением вершины, тензор Риччи равен нулю. В вершине имеется расходимость, связанная с расходимостью плотности энергии точечного тела.
Обычно связь между массой (которая пропорциональна коэффициенту в кривизне, задаваемой
Можно было бы рассмотреть некоторое распределение массы в ограниченной области и выяснить, как будет меняться α, когда размер области стремится к нулю. Однако мы будем действовать противоположным образом, что избавит нас от необходимости решать уравнения Эйнштейна. Деформируем коническую поверхность, «сгладив» вершину в сферический сегмент радиуса r, и выясним, какому распределению масс соответствует такое пространство.
Известно, что скаляр кривизны двумерной поверхности равен удвоенной гауссовой кривизне:
$$R = {2 K} = {2 \over r_1r_2},$$
где r1 и r2 — главные радиусы кривизны поверхности. Для сферической поверхности радиуса r скаляр кривизны R = 2/r2.
Установим некоторые геометрические соотношения. Длина окружности в основании конуса равна $$2\pi|AB|=2\pi\rho\sin\beta$$, длина той же линии на развертке конуса равна $$2\pi\alpha|AP|=2\pi\alpha\rho$$, откуда $$\alpha=\sin\beta$$. Тогда площадь $$S=2\pi r\cdot |BC|$$ сферического сегмента высоты $$|BC|=h=r(1-\sin\beta)$$ выражается как $$2\pi r^2(1-\alpha)$$.
Проинтегрируем (2):
$$\int T \sqrt{-g}\, d^2x =- {c^4 \over 16\pi G}\int R \sqrt{-g}\, d^2 x=-{c^4 \over 16\pi G}RS = -{c^4 \over 4G} (1- \alpha).$$
Учитывая аддитивность массы (отсутствие гравитационного дефекта массы следует из того, что тензор Римана в пустом пространстве нулевой и пространство локально галилеево; мы обсудим это ниже), получаем
$$mc^2 =\int {T_{00}} \sqrt{-g}\, d^2x=-\int T \sqrt{-g}\, d^2x={c^4 \over 4G} (1-\alpha) ,$$
$$\alpha =1-{4Gm \over c^2}.$$
Интеграл от скаляра кривизны по поверхности не зависит от размера области «сглаживания», поэтому полученный результат справедлив и для точечной массы, когда r → 0. Как видим, для обычных тел с положительной массой α < 1. Видно также, что масса рассматриваемого тела не может превышать величину c2/4G.
Геодезические
Решая систему уравнений для геодезических
$$\frac{d^2x^\lambda }{d s^2} + \Gamma^{\lambda}_{~\mu \nu }\frac{dx^\mu }{d s}\frac{dx^\nu }{d s} = 0,$$
которая в наших координатах принимает вид
$$\left\{ \begin{array}{l}\ddot{\varphi} + \dfrac{2}{r}\dot{r}\dot{\varphi}=0, \\ \ddot{r}-r\dot{\varphi}^2\alpha^2=0, \\ \end{array} \right. $$
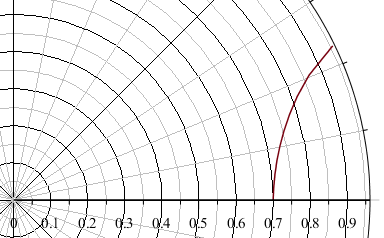
легко убедиться в том, что геодезические для пространства с точечной массой — это прямые $$r\sim 1/\sin(\alpha\varphi)$$ на развертке конуса.
Можно спроецировать геодезические на плоскость, перпендикулярную оси конуса. Тогда получится, что точечная масса «искривляет» пространство, или «отклоняет» движущиеся частицы. Однако легко видеть, что угол «отклонения» не зависит от прицельного параметра. Таким образом, уравнения Эйнштейна в (2+1) не содержат ньютоновское тяготение как предельный случай.
Более того, как показывает изучение геодезических, в определенном смысле гравитационное взаимодействие в (2+1) отсутствует. Как видно из вышеприведенной системы, для любых r0 и φ0 «кривая» покоя r = r0, φ = φ0 является геодезической. В обычном четырехмерном случае это не так. Например, для шварцшильдовского решения не существует такой системы координат, в которой тело в любой точке оставалось бы в покое.
Обобщения
Мы убедились в том, что точечной массе в трехмерном
Помимо бесконечной двумерной поверхности, можно представить еще и замкнутую поверхность, топологически эквивалентную сфере. Очевидно, масса такой замкнутой Вселенной есть c2/2G. Сфера будет реализовываться в случае равномерного распределения вещества. Дискретные массы будут образовывать многогранники. Например, восемь одинаковых материальных точек могут дать куб.
Комментарии
Например, о возможном (или не возможном) изменении меры стабильности атомов по отношению к
При этом он добавил, что коэффициент пересчёта массы в энергию (квадрат скорости света) повержен изменчивости под влиянием изменения гравиполя, что сильно удивило некоторых знатоков.
Так что, есть смысл осветить здесь и сейчас этот тезис подробнее и сделать вытекающие из него выводы…
В обычном
Ландавшица у меня под рукой нет. А в МТУ нет чётких указаний на то, что в ОТО прописан гравитационный дефект массы. В ранних работах Эйнштейна он точно был, но действительно ли он потом вошёл в состав ОТО?
Из самых общих соображений (сохранения энергии) в гравистатике должен быть либо гравитационный дефект массы, либо изменение коэффициента пересчёта массы в энергию.
Я не большой специалист в ОТО, но в процессе объяснения некоторых закономерностей в космологии возникла нестандартная метрика Шварцшильда, по типу рассмотренной Вами:
$$d{{s}^{2}}=\left( 1-\frac{{{r}_{S}}}{r} \right){{c}^{2}}d{{t}^{2}}-\frac{d{{r}^{2}}}{1-\frac{{{r}_{S}}}{r}}-\frac{1}{4}{{r}^{2}}\left( d{{\theta }^{2}}+{{\sin }^{2}}\theta \ d{{\phi }^{2}} \right)$$
Стандартная метрика Шварцильда проблему не решает.
Как трактовать возникший множитель 1/4?
Возможно ли его рассматривать как компенсация за спин 2 гравитационного поля, так чтобы на плоскости theta = pi / 2, возврат в исходную точку происходил за phi = 2 pi?
С уважением,
Канторович
Обычная шварцшильдовская метрика без посторонних коэффициентов тоже ведь возникает в ОТО.
Оставьте свой комментарий