Брахистохрона и свободное падение зарядов в дополнительном магнитном поле

Вернемся к задаче о брахистохроне — кривой скорейшего спуска. Иоганн Бернулли доказал, что в однородном поле тяжести такой кривой является циклоида.

Есть еще одна задача на движение частиц, в которой ответом тоже является циклоида, — задача о падении заряда в однородном магнитном поле. Эта задача эквивалентна движению заряженной частицы в ортогональных однородных электрическом и магнитном поле с нулевой начальной скоростью. Ее можно решать переходом в движущуюся систему отсчета, в которой электрическое поле зануляется и частица движется по окружности в магнитном поле. Комбинация поступательного движения по прямой и вращательного движения по окружности и дает циклоиду.

$$ \begin{tikzpicture}[scale=0.5] \draw[->] (-0.5,0) -- (20.5,0) node[right] {\( x \)}; \draw[->] (0,0.5) -- (0,-4) node[below] {\( y \)}; \foreach \x in {1,3.1,...,20} { \foreach \y in {0.5,-0.9,...,-4} { \draw[thick,blue] (\x,\y) node {\small\(\otimes\)}; } } \node[blue] at (-1,-3.5) {\(\vec{B}\)}; \draw[->,thick,red] (-1,0.5) -- +(0,-2) node[below] {\( \vec{E} \)}; \draw[thick,smooth,samples=100,domain=0:18.7] plot({\x-sin(deg(\x))},{cos(deg(\x))-1}); \foreach \x in {2,8.29,...,20} \draw[->,thick] ({\x-sin(deg(\x))}, {cos(deg(\x))-1}) -- ++(0.2, -0.1); \end{tikzpicture} $$

В прошлый раз мы занимались брахистохроной в центрально-симметричном силовом поле с потенциалом $$r^2$$ и обсудили, что ответом является дуга гипоциклоиды. Можно задать аналогичный вопрос и о свободном движении заряженной частицы: какова траектория заряда в потенциале $$r^2$$ и однородном магнитном поле, перпендикулярном плоскости движения заряда?

Из качественных соображений понятно, что траектория будет «звездообразной». Во-первых, заряд действительно всегда движется в одной плоскости, так как нет сил, не лежащих в этой плоскости. Во-вторых, когда заряд отпускают, он начинает двигаться к центру притяжения. По мере роста скорости увеличивается и магнитная сила, направленная перпендикулярно траектории и отклоняющая заряд в сторону. Заряд разворачивается, тормозится и останавливается на том же расстоянии от центра, на котором он был в начальном положении. Дальше этот цикл повторяется.

Численное решение уравнений движения показывает траекторию, очень напоминающую гипоциклоиду. Давайте разберемся, действительно ли заряд в магнитном поле и потенциале $$r^2$$ будет двигаться по гипоциклоиде и случайно ли траектория опять совпадает с брахистохроной?

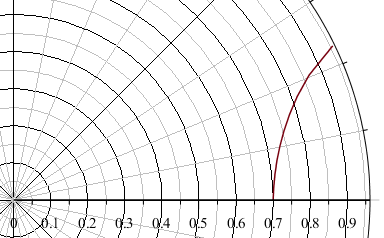
Падение в «вертикальном» поле

Направим ось y вниз и будем рассматривать движение в поле с потенциальной энергией $$U(x,y,z)=-mf(y)$$, причем $$f(0)=0$$. Из закона сохранения энергии $$v^2=2f(y)$$. Брахистохрона дается минимизацией интеграла для времени движения:

$$t=\int {dl\over v}=\int {\sqrt{dx^2+dy^2\over 2f(y)}}={1\over\sqrt{2}}\int {\sqrt{y'^2+1\over f(y)}}\ dx.$$

Первый интеграл соответствующего уравнения Эйлера — Лагранжа имеет вид

$$\frac{1}{K_1^2} = (y'^2 + 1) f(y).$$(1)

Это дифференциальное уравнение для $$f(y)=gy$$ описывает циклоиду.

Рассмотрим теперь свободное движение заряда в том же потенциале и горизонтальном магнитном поле (в этой системе координат оно направлено вдоль оси z). Выберем векторный потенциал в виде $$\vec{A}=(-yB,0,0)$$. Лагранжиан заряженной частицы в однородном магнитном поле

$$L={mv^2\over 2}-U+q\vec{v}\cdot\vec{A}= \frac{m}{2}\left(\dot{x}^2+\dot{y}^2\right)+mf(y)-qB\dot{x}.$$

Лагранжиан не зависит от времени и координаты x, поэтому энергия и обобщенный импульс сохраняются:

$$p_x = m \dot{x} - q B y,\quad E = \dfrac{m}{2}\left( \dot{x}^2 + \dot{y}^2 \right) - mf(y).$$

В начальном положении энергия и импульс равны нулю, поэтому:

$$\begin{cases} 0=m\dot{x}-qBy,\\ 0=\cfrac{1}{2}\left(\dot{x}^2 + \dot{y}^2\right)-f(y). \end{cases} \Leftrightarrow \begin{cases} \dot{x}&=\dfrac{qB}{m}y,\\ f(y)\!\!\!\!&=\cfrac{1}{2}\left(\dot{x}^2 + \dot{y}^2\right). \end{cases}$$

$$f(y)={1\over2}\dot{x}^2(y'^2+1)={q^2B^2\over 2m^2}y^2(y'^2+1).$$(2)

Полученное дифференциальное уравнение (2) траектории заряда в поле притяжения и магнитном поле совпадает с уравнением брахистохроны (1) только если $$f(y)\sim y$$. Таким образом, свободное движение в силовом и магнитном полях имеет ту же траекторию, что и брахистохрона в силовом поле, только если это однородное поле.

Падение в центральном поле

В прошлый раз мы находили уравнение брахистохроны в поле с потенциалом $$g(r)\sim r^2$$. Если проделать те же выкладки для произвольного потенциала, получим следующее дифференциальное уравнение:

$$k^2\left(r'^2+r^2\right)\left(g(r_0)-g(r)\right)=r^4.$$(3)

Перейдем теперь к свободному движению заряда в этом поле и дополнительном магнитном поле.

$$\usetikzlibrary{calc} \begin{tikzpicture}[scale=1.25] \foreach \x in {-2.3,-0.8,...,3} { \foreach \y in {-2.3,-0.8,...,3} { \draw[thick,blue] (\x,\y) node {\small\(\odot{}\)}; } } \draw[->] (0,0) -- (2.5,0) node[right] {$x$}; \draw[] (0,0) circle (2); \def\a{0.3} \def\b{2} \newcommand{\xt}[1]{(\b-\a)*cos(#1)+\a*cos((\b-\a)*#1/\a} \newcommand{\yt}[1]{(\b-\a)*sin(#1)-\a*sin((\b-\a)*#1/\a} \draw[thick,domain=0:110,smooth,variable=\t,samples=100] plot ({\xt{\t}},{\yt{\t}}); \def\t{25} \def\q{25.1} \coordinate (P) at ({\xt{\t}},{\yt{\t}}); \coordinate (P1) at ({\xt{\q}},{\yt{\q}}); \draw[->] (0,0) -- (P) node[midway,above] {$r$}; \draw[->] ($(P)!0!(P1)$) -- ($(P)!130!(P1)$) node[left] {$\vec{v}$}; \draw[->] (0.95,0) arc (0:22:0.95); \node at (1.1,0.2) {$\theta$}; \end{tikzpicture}$$

В силу наличия вращательной симметрии удобно выбрать векторный потенциал в форме $$\vec{A}=\vec{B}\times\vec{r}/2$$. Лагранжиан заряженной частицы

$$L={mv^2\over 2}-U+q\vec{v}\cdot\vec{A}= \frac{m}{2}\left(\dot{r}^2+r^2\dot{\varphi}^2\right)-mg(r)+{qB\over2}r^2\dot{\varphi}.$$

Первые интегралы для уравнения Эйлера — Лагранжа дают сохранение энергии и обобщенного момента импульса:

$$\begin{cases} \dfrac{2E}{m}\!\!\!\!&=r^2\dot{\varphi}^2+\dot{r}^2+2g(r),\\ L&=r^2(m\dot{\varphi}+\dfrac{1}{2}qB). \end{cases}$$

Так как в начальный момент $$r(0)=r_0$$, а скорость равна нулю, то:

$$\begin{cases} 2g(r_0)\!\!\!\!&=r^2\dot{\varphi}^2+\dot{r}^2+2g(r),\\ r_0^2\dfrac{1}{2}qB\!\!\!\!&=r^2(m\dot{\varphi}+\dfrac{1}{2}qB). \end{cases} \Leftrightarrow \begin{cases} 2g(r_0)-2g(r)\!\!\!\!&=\dot{\varphi}^2(r^2+r'^2),\\ \dot{\varphi}r^2&=(r_0^2-r^2)\dfrac{qB }{2m}. \end{cases}$$

$$2(g(r_0)-g(r))=(r^2+r'^2)\left({r_0^2\over r^2}-1\right)^2\dfrac{q^2B^2}{4m^2}.$$(4)

Перемножив (3) на (4), получаем

$$2k^2\left(g(r_0)-g(r)\right)^2=\left(r_0^2 - r^2\right)^2\dfrac{q^2B^2}{4m^2}.$$

Мы видим, что только при $$g(r)\sim r^2$$ уравнения (3) и (4) совместимы.

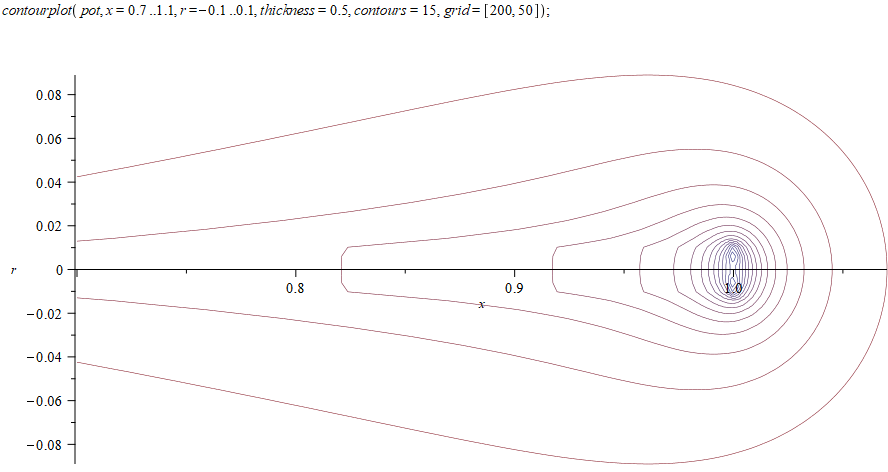
Совпадение брахистохроны и траектории падения заряженной частицы в дополнительном магнитном поле оказалось случайным. Оно имеет место для для однородного поля притяжения и для осцилляторного потенциала в центрально-симметричном случае. Для других потенциалов дифференциальные уравнения различаются, поэтому совпадения не будет.