Брахистохрона под землей

Мотивация

В сборниках задач по физике часто встречается известная задача о свободном падении тела сквозь прямой тоннель, проходящий через центр Земли и соединяющий диаметрально противоположные точки. Для решения нужно знать, что сила притяжения к центру Земли в таком тоннеле уменьшается линейно до нуля, и тело, упавшее в такой тоннель, будет совершать гармонические колебания. Время движения составляет половину периода и для модели однородной Земли составляет 42 минуты. Более того, это время не меняется для любого прямого тоннеля, идущего по хорде (не проходящего через центр), если трением можно пренебречь.

Также в популярных книгах и других источниках есть задача о брахистохроне — кривой скорейшего спуска. В ней требуется найти форму желоба, проложенного между двумя фиксированными точками A и B, чтобы время скатывания тела из A в B было наименьшим. В однородном гравитационном поле брахистохроной является дуга циклоиды.

Вполне естественным кажется желание скрестить эти две задачи и выяснить, какой формы нужно проложить тоннель под землей, чтобы в идеальной ситуации без трения между точками A и B на поверхности (скажем, между двумя городами) поезд проезжал за наименьшее время. Эта новая задача имеет аналитическое решение. Её ответом является гипоциклоида — кривая, которую описывают точки окружности радиуса $$a$$, катящейся без проскальзывания внутри другой окружности радиуса $$b$$. Вот как записывается параметрическое уравнение гипоциклоиды и выглядит ее чертеж:

$$\left\{\begin{array}{lr} x=(b-a)\cos \theta+a\cos(b-a)\theta,\\ y=(b-a)\sin\theta-a\sin(b-a)\theta. \end{array}\right.$$

$$\begin{tikzpicture} \def\clr{black} \def\a{1} \def\b{5} \newcommand{\xt}[1]{(\b-\a)*cos(#1)+\a*cos((\b-\a)*#1/\a} \newcommand{\yt}[1]{(\b-\a)*sin(#1)-\a*sin((\b-\a)*#1/\a} \draw[cyan,very thin] (-\b-1,-\b-1) grid (\b+1,\b+1); \draw[->] (-\b-1,0) -- (\b+1,0); \draw[->] (0,-\b-1) -- (0,\b+1); \draw[\clr,thick] (0,0) circle (\b); \draw[\clr,dashed,very thin] (0,0) circle (\b-\a); \draw[line width=2pt,orange!80!red] plot[samples=60,domain=0:\a*360,smooth,variable=\t] ({\xt{\t}},{\yt{\t}}); \def\t0{40} \draw[\clr!50!black] (\t0:\b-\a) circle (\a); \draw[purple,fill] ({\xt{\t0}},{\yt{\t0}}) circle (2pt) -- (\t0:\b-\a) circle (1pt) node [midway, sloped, above] {\scriptsize $a$} -- (0,0) circle (1pt) node [midway, sloped, above] {\scriptsize $b-a$} node [below right] {$O$}; \node[\clr,fill=white,text width=1cm,align=center] at (-\b,\b) {$a=\a$ $b=\b$}; \end{tikzpicture}$$

Я задумался об этой задаче в старших классах или на первом курсе института, но тогда, разумеется, у меня не хватало знаний для решения в аналитическом виде. Я вернулся к задаче на четвертом курсе и смог довести вычисления до конца, не обращаясь к источникам, но и не без помощи Maple. Эти вычисления были одними из самых сложных среди всех задач с явным аналитическим ответом, которые я решал.

Физическая сторона задачи

$$\begin{tikzpicture} \def\a{1} \def\b{5} \draw ([shift=(-10:\b)]0) arc (-10:90:\b); \draw[-stealth] (\b,0) node[right]{$A$} -- node[pos=0.92,above,inner sep=2] {$\varphi$} (0,0) -- (\b*0.35,\b*0.6) node[below,pos=0.9]{$\vec{r}$} ; \node[above] at (\b*0.32,\b*0.95) {$B$}; \draw[line width=1pt,orange!80!red] plot[samples=12,domain=0:72,smooth,variable=\t] ({(\b-\a)*cos(\t)+\a*cos((\b-\a)*\t/\a},{(\b-\a)*sin(\t)-\a*sin((\b-\a)*\t/\a}); \end{tikzpicture}$$

Движение поезда по подземному тоннелю будем рассматривать в полярных координатах. Считаем потенциал внутри Земли осцилляторным: $$U\sim r^2$$. Запишем закон сохранения энергии с учетом нулевой скорости поезда на поверхности:

$${mv^2\over 2}+{m\omega^2r^2\over 2}={m\omega^2r_0^2\over 2},$$(1)

где $$r_0$$ — радиус Земли, $$\omega=2\pi/T$$ — круговая частота колебаний, соответствующая периоду в 84 минуты. Время движения через тоннель $$\inline t=\int{dl\over v}$$. Выражаем скорость $$\inline v=\omega\sqrt{r_0^2-r^2}$$ из (1) и для времени движения поезда через тоннель получаем следующее выражение:

$$t=\int{dl\over v}={1\over\omega}\int{\sqrt{dr^2+r^2d\varphi^2}\over\sqrt{r_0^2-r^2}}={1\over\omega}\int{\sqrt{r'^2+r^2}\over\sqrt{r_0^2-r^2}}d\varphi,$$

Здесь мы выразили элемент длины пути через полярные координаты. Таким образом, задача свелась к поиску функции $$r(\varphi)$$ с фиксированным значением $$r(\varphi_A)=r(\varphi_B)=r_0$$ на концах отрезка, для которой функционал

$$\omega t=\int\limits_{\varphi_A}^{\varphi_B}\sqrt{{r'^2+r^2}\over{r_0^2-r^2}}d\varphi$$(2)

принимает наименьшее значение.

Математическая сторона задачи

Задача по минимизации интеграла (2) на множестве достаточно хороших с точки зрения физика функций (скажем, дифференцируемых сколько нужно раз) — типовая задача вариационного исчисления. Заметим, что подынтегральное выражение в (2) можно представить в виде функциональной зависимости от $$r$$ и ее производной:

$${\cal L}(r,r')=\sqrt{{r' ^2+r^2}\over{r_0^2-r^2}}$$(3)

Из курса дифференциальных уравнений известно, что экстремальные значения (2) нужно искать на решениях дифференциального уравнения Эйлера — Лагранжа:

$${\partial{\cal L}\over\partial r}-{d\over d\varphi}{\partial{\cal L}\over\partial r'}=0.$$

Если вы вооружитесь бумагой и ручкой и попробуете подставить сюда (3), то быстро заметите сложность получившегося дифференциального уравнения со второй производной и нагромождением корней и осознаете тупиковость этого подхода. В системах компьютерной алгебры есть встроенные пакеты для решения вариационных задач. Вот пример для Maple, где вы видите трехэтажное дифференциальное уравнение:

Кроме того, Maple заботливо подсказывает, что у получившегося дифференциального уравнения есть первый интеграл. И тут вы вспоминаете, что на курсах теоретической механики и дифференциальных уравнений всё-таки рассказывают некоторые полезные вещи. В частности, у уравнений Эйлера — Лагранжа есть интегралы движения. В нашем случае интеграл движения имеет вид

$${\cal L}-r'{\partial{\cal L}\over\partial r'}=const.$$

Если вам проще воспринимать физику, а не математику, вы можете представить некоторую систему, описываемую функцией Лагранжа (3). Движение во «времени» $$\varphi$$ от «момента» $$\varphi_A$$ к $$\varphi_B$$ будет происходить по такой траектории $$r(\varphi)$$, на которой «действие» (2) примет экстремальное значение. Так как функция Лагранжа $$\cal L$$ не зависит от «времени» $$\varphi$$, то у системы есть сохраняющаяся величина — «энергия». Первый интеграл выше как раз и дает величину этой «энергии».

Выполним дифференцирование:

$$k={\cal L}-r'{\partial{\cal L}\over\partial r'}=\sqrt{{r' ^2+r^2}\over{r_0^2-r^2}} -r'{r'\over\sqrt{r_0^2-r^2}\sqrt{r'^2+r^2}}={r^2\over\sqrt{r_0^2-r^2}\sqrt{r'^2+r^2}}.$$

Мы пришли к дифференциальному уравнению первого порядка $$\inline r^2=k\sqrt{r'^2+r^2}\sqrt{r_0^2-r^2}$$, в котором разделяются переменные и получается следующий интеграл:

$$\varphi=\int{dr\over\sqrt{\cfrac{r^4}{k^2(r_0^2-r^2)}-r^2}}.$$

Его можно вычислить аналитически. Например, Maple выдает такой результат:

Чтобы доказать, что это выражение описывает гипоциклоиду, нужно взять её параметрическое уравнение и проделать достаточно громоздкие преобразования обратных тригонометрических функций, которые я не буду сейчас приводить.

В интернете опять кто-то неправ, или учимся избегать ошибок

Когда я занимался этой задачей, мне попадалась статья с нестандартными вычислениями: вместо полярных координат использовались декартовы. Тогда мне показалось, что автору очень повезло: уравнение гипоциклоиды в параметрической форме написано в таком виде, что параметр оказался пропорциональным физическому времени. При подготовке этой заметки я опять наткнулся на ту же статью. Сейчас эти нестандартные вычисления кажутся мне ошибочными.

Я предположил, что это чья-то студенческая работа с не очень высокими требованиями. Решил подробнее узнать об авторе, Аманде Максхэм, и нашел заметку в ее блоге как раз об этой статье. Она пишет, что эта статья выдается на первой странице в гугле по запросу «gravity train». Раз так, то тем более нужно разобраться, скрывается ли за нестандартными вычислениями какой-то хитрый прием, или это просто ошибка. Причем моя цель не в том, чтобы показать, что в интернете опять кто-то неправ, а в том, чтобы научиться отличать правильный способ рассуждения от неправильного.

Вот ключевой момент статьи, в котором делается попытка доказать, что гипоциклоида — искомое решение:

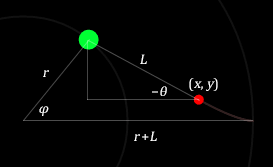
Вопросы начинаются с формулы (19), в которой пропущен дифференциал, и поэтому не совсем понятно, по какому параметру дальше берутся производные. Эти же производные сохраняются вплоть до (22), куда подставляются $$x(t)$$ и $$y(t)$$ из (24) и (25). Но параметр $$t$$ в (24) и (25) не может быть временем $$t_\text{физ}$$, так как он является аргументом тригонометрических функций и должен быть безразмерным. Получается, это некоторый параметр, задающий положение точки на траектории, но не являющийся временем.

(Попутно возникает мини-вопрос о том, откуда взялась разность $$x'^2-y'^2$$ вместо соответствующей суммы в правых частях (20) и (21), но эта опечатка в четырех местах не распространяется на дальнейшие рассуждения, и мы к ней придираться не будем.)

Еще возникает вопрос о степенях свободы. В уравнениях (19) и (22) неизвестные величины — $$(x, y, t)$$. Таким образом, эти уравнения содержат лишнюю степень свободы по сравнению с неизвестными $$(r, \varphi)$$ из нашего рассмотрения (и из предыдущего раздела работы Аманды). Эта избыточность мешает корректному применению формализма Лагранжа — Эйлера. Какие признаки этого мы видим?

1. (22) — не единственное возможное следствие из (20) и (21). Если поделить (20) на (21), получим, что $$(y'/x')^2=(dy/dx)^2=const$$, а это есть уравнение, описывающее не гипоциклоиду, а прямую траекторию. Почему это следствие из (20) и (21) менее правильное, чем (22)?

2. (22) с точностью до константы $$C$$ по форме совпадает с законом сохранения энергии, с которого начиналось решение. Действительно, выражение в левой части напоминает квадрат скорости, а в правой — разницу квадратичных потенциалов, то есть изменение потенциальной энергии. Присутствие константы $$C$$ объясняется тем, что производные в (22) берутся не по физическому времени $$t_\text{физ}$$, а по другому параметру $$t$$, который в $$C$$ раз меньше: $$t_\text{физ}=Ct$$. Если бы связь $$t_\text{физ}=Ct$$ нарушилась, то (22) противоречило бы закону сохранения энергии. Таким образом, (22) можно получить без применения лагранжева формализма, просто напрямую из закона сохранения энергии с помощью замены $$t_\text{физ}=Ct$$. Следовательно, (22) не может иметь большего физического содержания, чем закон сохранения энергии, и не несет информацию о траектории, минимизирующей время.

3. (24) и (25) формально являются решением (22), так как зануляют его при выполнении (26). Но они не являются единственным решением. Фактически, любое физически возможное движение из-за сохранения энергии будет удовлетворять уравнению (22). Важно лишь выбрать параметризацию этого движения так, чтобы физическое время было пропорционально параметру. Возьмем для примера движение по хорде $$x(t)=A$$, $$y(t)=B\cos t$$, где $$\inline A^2+B^2=R^2$$, подставим в (22) и при должном выборе константы $$C$$ (то есть при выборе правильного движения во времени вдоль хорды) получим тождество:

$$RB^2\sin^2 t=gC^2(R^2-A^2-B^2\cos^2 t)=gC^2B^2\sin^2 t.$$

Таким образом, осцилляторное движение по тоннелю в виде прямой хорды также является решением (22). Но оно отнюдь не минимизирует функционал (19) для общего времени движения между двумя точками.

Я так и не смог понять, можно ли провести рассуждения в декартовых координатах с избыточной степенью свободы и получить правильный ответ. Понятно желание использовать декартовы координаты, а не полярные, так как в них уравнение гипоциклоиды выглядит проще. Но интуитивно кажется, что лишняя степень свободы, появившаяся в функционале времени и соответствующая выбору закона движения тела вдоль траектории, не дает при применении лагранжева формализма достаточных ограничений на траекторию.

Я оставил комментарий в блоге Аманды с вопросами. Но никакой реакции не последовало.

Напишите свой комментарий, если видите ошибку в моих рассуждениях, или если знаете, как сделать корректное рассмотрение в декартовых координатах.

Добавлено 13.10.2023: я нашел у себя в архиве файлов сохраненную в 2008 году статью о брахистохроне, и это не работа Аманды. Автор не указан, статья располагалась по этой ссылке. Ход решения в этих статьях одинаков, но видно, что написаны они по-разному, и, похоже, разными авторами. «Опечаток» в этой статье меньше, но иногда дифференциал под интегралом тоже пропадает. Разумеется, критика идеи решения относится в равной мере и к этой статье.