Как создается электрическое поле в проводнике с током?

Мотивация

Вопрос, вынесенный в заголовок, в свое время породил большую дискуссию на физическом форуме (1, 2, 3). Вот более точная формулировка вопроса:

Рассмотрим длинный провод, подключенный к батарейке. По нему течет постоянный ток. Ток создается электрическим полем Е, которое, в свою очередь, создается зарядами на полюсах батарейки. Почему вдали от полюсов (например, в середине проводника) поле Е=const, а не убывает при удалении от полюсов, как ему положено по закону Кулона?

Правильный ответ заключается в том, что батарейка не является единственным источником электрического поля, какие бы процессы в ней ни происходили. На поверхности проводника с током возникают дополнительные заряды, которые и создают постоянное электрическое поле внутри.

Обоснование появления зарядов на поверхности проводника с током следующее. Плотность тока внутри проводника по закону Ома пропорциональна напряженности поля:

$$\vec{j}=\lambda \vec{E}.$$

Возьмем дивергенцию обеих частей и воспользуемся первым уравнением Максвелла $$\text{div}\vec{E}=4\pi\rho$$ и законом сохранения электрического заряда в локальной форме $$\text{div}\vec{j}=-\partial\rho/\partial t$$:

$$-{\partial\rho\over\partial t}=4\pi\lambda\rho.$$(1)

Так как протекание тока — стационарный процесс, в котором величины со временем не меняются, то производная в левой части зануляется, поэтому правая часть — плотность зарядов внутри проводника — тоже есть 0. Следовательно, поле в проводнике может создаваться только зарядами на его поверхности.

Почему-то у этого простого обоснования есть противники, которые утверждают, что появление постоянного электрического поля вдоль проводника нельзя объяснить в классической электродинамике, и изобретают свои объяснения, например: источник тока создает избыток электронов с одного конца провода, и эти лишние электроны «расталкивают» другие электроны. Физического содержания в этих объяснениях нет, и мы не будем их рассматривать.

В этом посте попробуем найти, каким именно должно быть распределение поверхностного заряда, чтобы внутри проводника с постоянным сечением создалось однородное электрическое поле.

Близкая задача из электростатики

К сожалению, мы не можем найти точное распределение поверхностных зарядов по проводнику, если не учтем механизм того, как именно создается разность потенциалов на его концах. Вместо выбора такого механизма сделаем приближение, сказав что никакого механизма нет. Фактически, будем решать упрощенную задачу: как нужно распределить заряд по поверхности, чтобы поле внутри стало таким же, как и при стационарном протекании тока?

Разумеется, распределенный по поверхности проводника заряд без механизма создания разности потенциалов сразу же растечется (характерное время растекания можно найти из уравнения (1)), и, казалось бы, решать такую задачу бессмысленно. Но можно сформулировать задачу из электростатики о проводнике во внешнем однородном электрическом поле с точно таким же ответом:

Цилиндрический проводник длины l и радиуса R помещен во внешнее электрическое поле, так что его ось направлена по полю. Найти распределение поверхностных зарядов.

Действительно, в этом случае заряды так распределятся по поверхности проводника, что линейный потенциал внешнего поля $$\varphi_\text{внеш}=-|E|x$$ будет скомпенсирован их собственным потенциалом $$\varphi=kx$$ во всем объеме проводника.

Для полноты отметим, что аналогичная задача проводнике сферической формы имеет простое точное решение.

Наивный подход

$$ \newcommand{\drawCircle}[3]{ \draw (#1,#2) arc (90:270:#3 and #2); \draw[dashed] (#1,-#2) arc (-90:90:#3 and #2); } \newcommand{\drawTik}[2]{\draw (#1,0.1) -- ++ (0,-0.2) node[fill=white,below,inner sep=0,pos=1.4] {$#2$}} \begin{tikzpicture}[>=latex] \def\rx{4} \def\xx{-1.9} \def\x{1.9} \def\ry{1.2} \def\e{0.48} \node[above right,inner sep=2] at (0,\ry) {$R$} \node[below right,inner sep=2] at (0,-\ry) {$-R$} \node[below right] at (0,0) {$0$} \draw[->,very thin] (-\rx-1,0) -- (\rx+1,0) node[below] {$x$}; \draw[->,very thin] (0,-1.5*\ry) -- (0,2*\ry) node[left] {$r$}; \draw (\rx,0) ellipse (0.48 and \ry); \draw[] (-\rx,-\ry) -- (\rx,-\ry) (-\rx,\ry) -- (\rx,\ry); \drawCircle{-\rx}{\ry}{\e} \drawCircle{\xx-0.1}{\ry}{\e} \drawCircle{\xx+0.1}{\ry}{\e} \node[above] at (\xx,\ry) {$dx_1$} \drawTik{\xx}{x_1} \drawTik{\x}{x} \draw[dashed](\xx,\ry) -- (\x,0) \draw (\rx,0) ellipse (0.25 and 0.62); \draw (\rx,0) ellipse (0.3 and 0.75); \drawTik{-\rx}{-{l\over2}} \drawTik{\rx}{l\over2} \draw[dashed] (\x,0) -- (\rx,0.68) node[inner sep=2,pin={[pin distance=6, pin edge={<-,solid,black},fill=white,inner sep=1]30:$dr$}] {} \draw[->] (2.8,\ry+0.8) -- ++(2,0) node[pos=0.9,above] {$\vec{E}$}; \end{tikzpicture} $$

Обозначим плотность зарядов через $$\sigma_1(x)$$ на боковой поверхности и $$\sigma_2(r)$$ на поверхности оснований. Через эти величины можно выразить электрическое поле или потенциал внутри цилиндра, взяв интегралы по поверхности. Скажем, на оси цилиндра

$$\varphi(x)=\int\limits_{-l/2}^{l/2}{2\pi R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}+ \int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r) \over\sqrt{r^2+\left(x-{l\over2}\right)^2}} -\int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r)\over\sqrt{r^2+\left(x+{l\over2}\right)^2}} =Ex.$$(2)

Здесь учтены симметрии задачи: вращательная симметрия вокруг оси повлияла на выбор элементов площади, а зеркальная симметрия выражается в том, что плотности зарядов на основаниях цилиндра имеют противоположный знак ($$\sigma_2$$ и $$-\sigma_2$$), и в том, что функция $$\sigma_1(x)$$ — нечетная.

Мы получили интегральное уравнение на $$\sigma_1(x)$$ и $$\sigma_2(r)$$. Я не смог решить его в явном виде. Можно было бы рассмотреть предельный режим, когда $$l\gg R$$, и поискать приближенное решение в области $$|x|\ll l$$. Тогда вкладом двух последних интегралов можно пренебречь, а в первом интегрировать от минус бесконечности до бесконечности:

$$\int\limits_{-\infty}^{\infty}{R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}=x.$$(3)

Здесь я опустил коэффициент пропорциональности, не влияющий на дальнейшие рассуждения. Это интегральное уравнение имеет вид свертки ядра $$k(x)=1/\sqrt{1+x^2/R^2}$$ и искомой функции. Такое уравнение можно решить, взяв преобразование Фурье от обеих частей:

$${\cal F}(\sigma_1)\int {e^{-ikx}\over\sqrt{1+\dfrac{x^2}{R^2}}}dx=\int xe^{-ikx}dx.$$

Интегрирование по частям справа дает $$\inline\int xe^{-ikx}dx=-i\delta(k)/k$$. Искомая функция ищется через обратное преобразование Фурье:

$$\sigma_1(x)={-i\over2\pi}\int\dfrac{\delta(k)e^{ikx} dk}{k\int {e^{-iks}\over\sqrt{1+\frac{s^2}{R^2}}}ds}.$$

Дельта-функция просто возвращает подынтегральное выражение при $$k=0$$. Интеграл в знаменателе можно выразить через модифицированную функцию Бесселя второго рода, и знаменатель стремится к 0 при $$k\to0$$. Получается, не существует «достаточно хорошей» функции $$\sigma_1(x)$$, определенной на всей вещественной оси, удовлетворяющей приближенному уравнению. Мы сделали слишком сильное упрощение, перейдя от уравнения (2) к уравнению (3).

Пока оставим попытки решить интегральное уравнение и посмотрим, что нам предлагает математика, а именно раздел, изучающий уравнения математической физики.

Аналитические методы заводят в тупик

Наша задача на языке математики формулируется так. Вне цилиндра потенциал подчиняется уравнению Лапласа $$\Delta\varphi=0$$ и стремится к нулю (как поле диполя) на бесконечности. На поверхности цилиндра потенциал фиксирован и описывается начальными условиями

$$\begin{align*}\varphi(x, R)&=Ex,\quad x\in\left[-{l\over2},{l\over2}\right],\\ \varphi\left(\pm{l\over2}, r\right)&=\pm E{l\over2},\quad r\in\left[0,R].\end{align*}$$

Это формулировка задачи Дирихле для уравнения Лапласа. Решение у этой задачи существует и оно единственно. Потенциал определяет электрическое поле вне цилиндра, а скачок нормальной составляющей электрического поля на границе цилиндра пропорционален искомой поверхностной плотности заряда.

Уравнение Лапласа в цилиндрических координатах с учетом цилиндрической симметрии задачи записывается так:

$${1\over r}{\partial\over\partial r}\left(r{\partial\varphi\over\partial r}\right)+{\partial^2\varphi\over\partial x^2}=0.$$(4)

Стандартный метод решения таких уравнений — метод разделения переменных, он же метод Фурье. Искомая функция ищется в виде суммы (конечной, счетной или интеграла) произведений функций, в которых каждый сомножитель зависит только от своей переменной:

$$\varphi(x,r)=\Sigma_kX_k(x)R_k(r).$$

Мы хотим, чтобы (4) выполнялось не только для всей суммы целиком, но и для каждого элемента $$X_k(x)R_k(r)$$. Подставляем его в (4) и получаем:

$${1\over rR_k}{\partial\over\partial r}(rR_k')=-{1\over X_k}X_k''=-\lambda_k.$$

После такой подстановки получилось представить равенство так, что левая его часть зависит только от координаты r, а правая — только от координаты x. Равенство возможно, только если никакой зависимости нет, то есть и правая, и левая часть равны некоторой константе $$\lambda_k$$. Дальше, в зависимости от вида граничных условий, выбирается одно из двух получившихся дифференциальных уравнений

$$\left\{ \begin{array}{l} R_k'+rR_k''+\lambda_krR_k=0,\\ X_k''-\lambda_kX_k=0,\end{array} $$

и исследуется задача Штурма — Лиувилля: при каких $$\lambda_k$$ с учетом граничных условий у этого дифференциального уравнения возможны решения. Наконец, для этих $$\lambda_k$$ решается оставшееся дифференциальное уравнение и ответ обычно записывается в виде ряда по собственным функциям оператора Штурма — Лиувилля.

Проделать эту процедуру в нашем случае не представляется возможным. Дело в том, что первое уравнение нужно решать на области $$r\in[R,\infty)$$, когда $$x\in\left[-{l/2},{l/2}\right]$$, и на области $$r\in[0,\infty)$$ в противоположном случае. Аналогично со вторым уравнением. Представить решение по всему пространству вне цилиндра в виде одного ряда по собственным функциям какой-либо задачи Штурма — Лиувилля не получается. Есть предложение разбить пространство на несколько частей (как минимум на 3, а то и на 5), решить задачу Дирихле в каждой из них, а затем сшивать эти решения вместе с производными, накладывая дополнительные условия на коэффициенты в рядах и выкидывая слагаемые, которые сшить нельзя. Я не стал заходить в эти дебри, тем более что ответ в виде непонятного ряда по функциям Бесселя вряд ли вызовет известное ощущение завершенности от решения задачи.

Численное решение

Возвращаемся к интегральному уравнению (2) из наивного подхода. Зададимся какими-нибудь конкретными значениями размеров. Пусть длина провода будет 10 сантиметров, а его диаметр — 1 миллиметр. В подходящих единицах измерения можно считать, что $$l=2$$, $$R=0,\!01$$, а коэффициент пропорциональности в уравнении (2) отсутствует. Таким образом, мы будем решать уравнение

$$\int\limits_{-1}^{1}{dx_1\,\sigma_1(x_1)\over\sqrt{1+10000(x-x_1)^2}}+ \int\limits_{0}^{0,01}r\,dr\,\sigma_2(r)\left({1 \over\sqrt{r^2+\left(x-1\right)^2}} -{1\over\sqrt{r^2+\left(x+1\right)^2}}\right) =x.$$

Приближение к его решению можно искать не на всех функциях, а на определенном классе функций, например, на нескольких первых слагаемых разложения в степенной ряд. Отклонение получающейся функции $$\widetilde{\varphi}_a(x)$$ от правой части будем оценивать как интеграл от квадрата разности, и будем подбирать параметры функций a, добиваясь минимума этого интеграла:

$$f(a)=\int\limits_{-1}^{1}\left(\widetilde{\varphi}_a(x)-x\right)^2dx\to \text{min}.$$

Как обычно, решение попробовал найти в Maple. У меня не получилось заставить его минимизировать такой интеграл, зависящий от набора параметров. Поэтому я оставлял только один параметр, заменяя остальные их текущими значениями, строил график по этому параметру и определял его текущее значение в минимуме. Фактически выполнял вручную итерации из метода координатного спуска для функции $$f(a)$$ такого типа:

f := a -> int((
   int((11.485*s + 0.584*s^3 + 0.883*s^5 + 0.587*s^7 + 0.2*s^9 + 3.57*s^11)/
      sqrt(1 + 10000*(x - s)^2), s = -1 .. 1, numeric) +
   int((5.01 + 5.46*10^2*r + 5.71*10^5*r^2 + 3.62*10^6*r^3 + 42.35*10^8*r^4 + a*r^5)*
      r*(1/sqrt(r^2 + (1 - x)^2) - 1/sqrt(r^2 + (x + 1)^2)), r = 0 .. 0.01, numeric)
- x)^2, x = -1 .. 1, numeric)

Здесь все интегралы отмечены как «numeric», чтобы Maple не пытался вычислить их аналитически. В моем случае попытка аналитического вычисления существенно замедляла работу, так что я не мог дождаться результата. Потенциал на оси для моего приближения на глаз отличается от прямой только у краев:

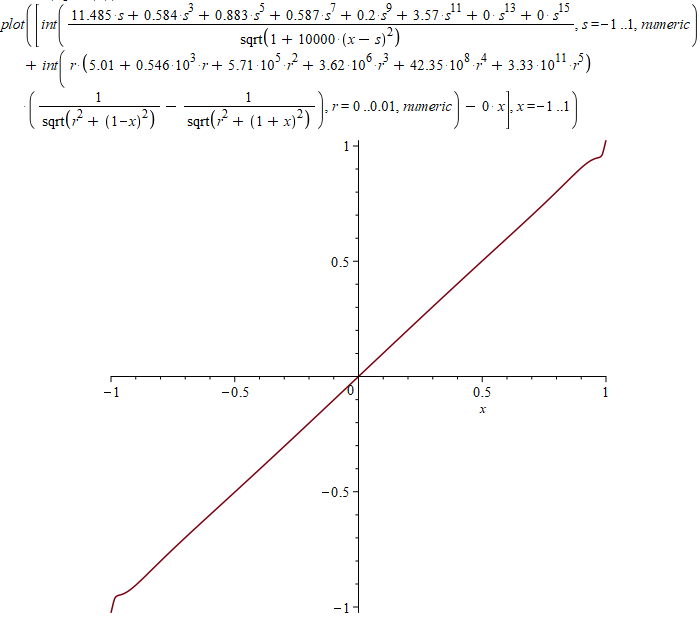
График отклонения от прямой (интеграл от квадрата этой функции я минимизировал, здесь масштаб по осям разный):

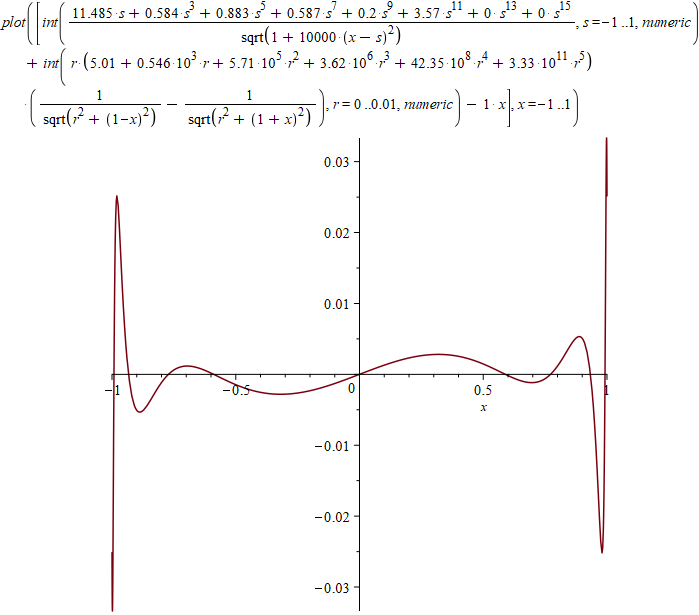
Можно также нарисовать графики плотностей на основаниях и на боковой поверхности:

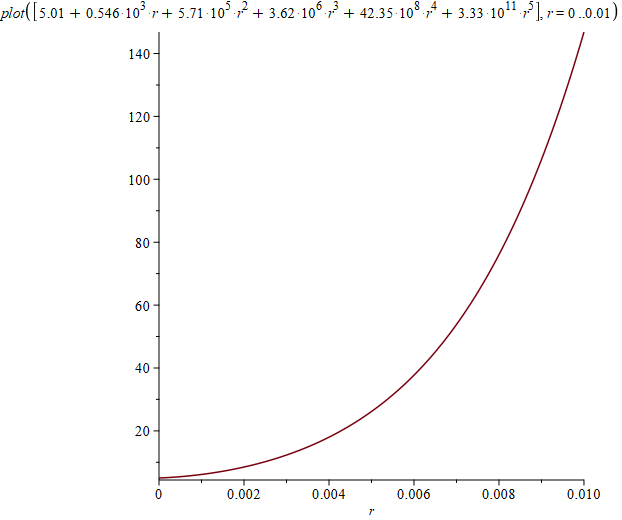
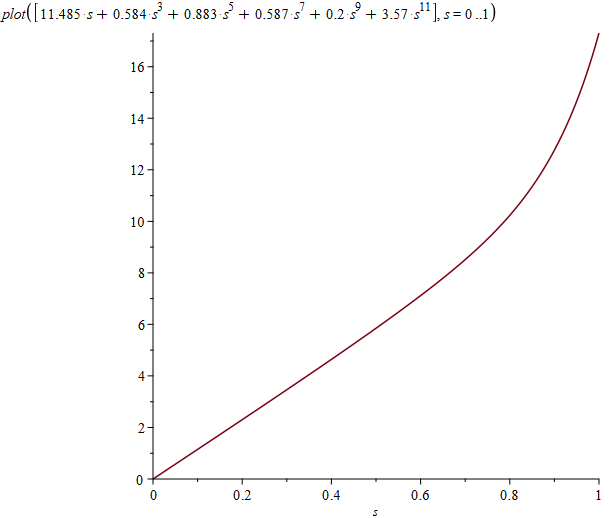
Перейдем теперь к исследованию этого решения по всему пространству. Чтобы найти потенциал в произвольной точке не на оси, нужно добавить интегрирование по углу, так как теперь расстояние от элемента поверхности до расчетной точки уже зависит от угла. Трехмерный график потенциала выглядит так:

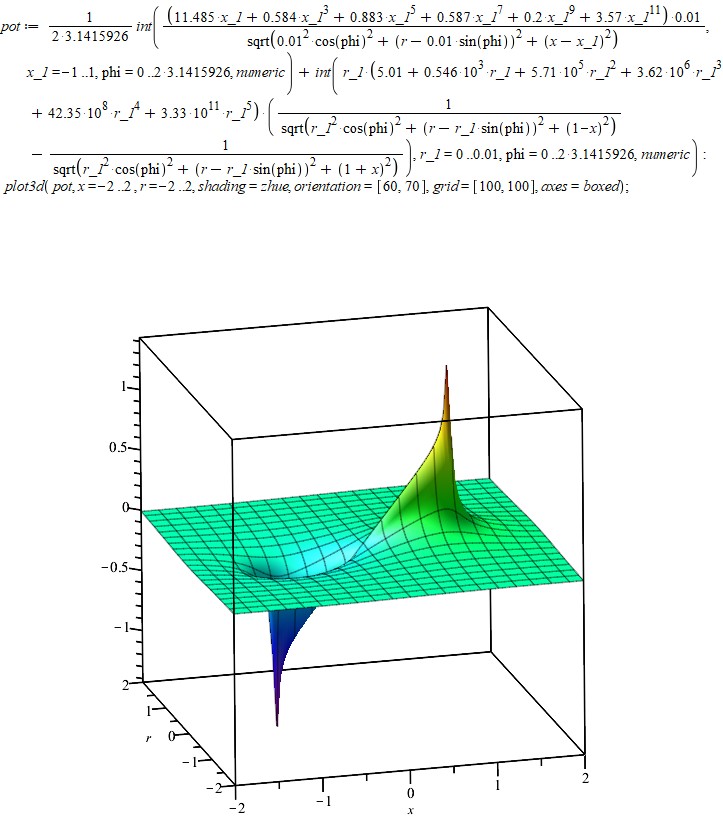
Нарисуем сечения эквипотенциальных поверхностей:

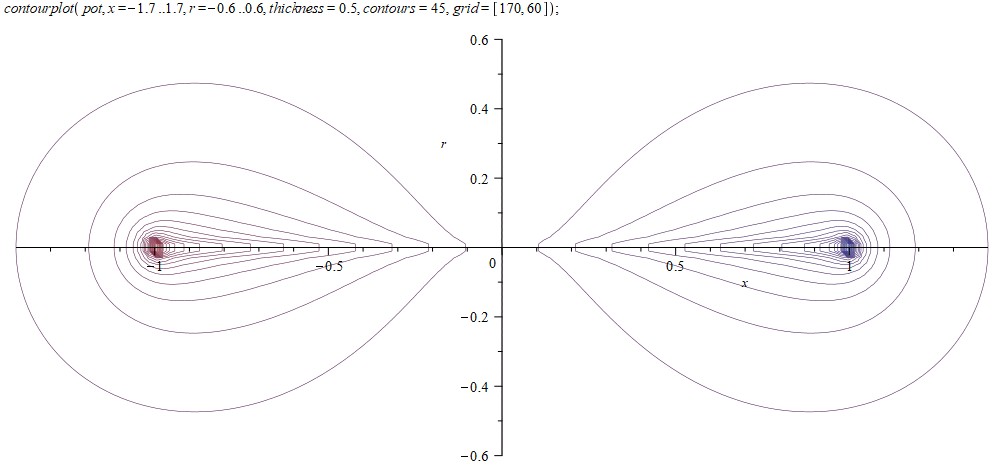
Рассмотрим поближе край проводника:

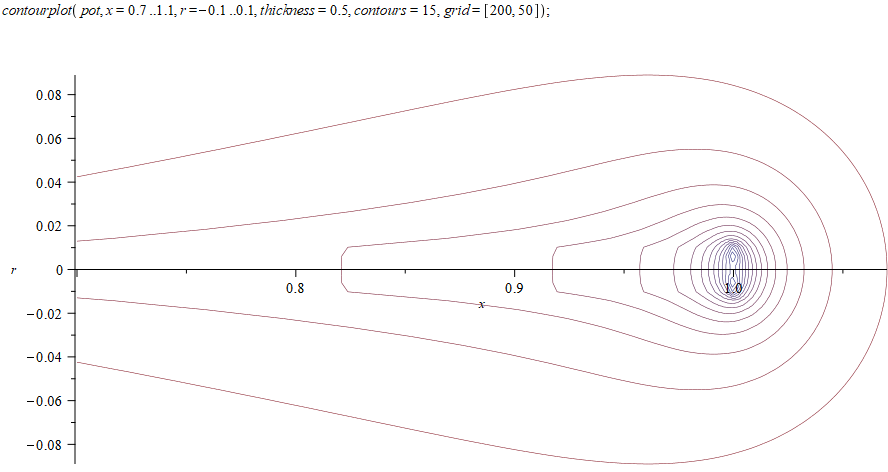
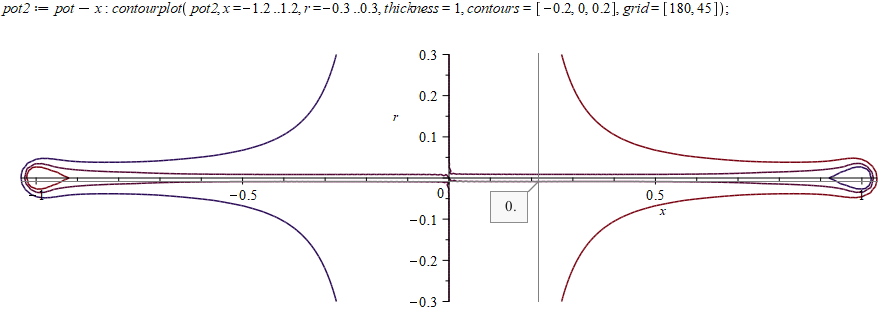
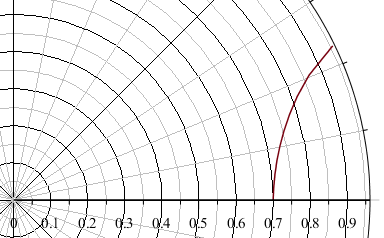
На полученный потенциал можно наложить внешнее электрическое поле и проверить, какая будет поверхность нулевого потенциала. Для правильного решения она должна совпадать с цилиндрической поверхностью проводника. В нашем случае у его краев (от 0,7 до 1) наблюдаются заметные утолщения, наглядно показывающие степень полученного приближения:

Вывод

Мы пытались решить две близких задачи: одна об электрическом поле внутри и снаружи провода с током, вторая о разделении зарядов в проводнике во внешнем электрическом поле. Аналитические методы не привели к успеху. Пришлось искать приближенное численное решение в Maple и использовать встроенные инструменты визуализации решения.

Из этого мини-исследования на третьем курсе получилась бы хорошая курсовая работа. Преподаватели урматов и вычматов были бы довольны.