Магнитные монополи, потоки энергии и квантование заряда

Мы уже рассчитывали замкнутые потоки энергии в стационарных полях зарядов и магнитов. Перейдем к более экзотическому примеру с участием не открытого на опыте магнитного монополя.

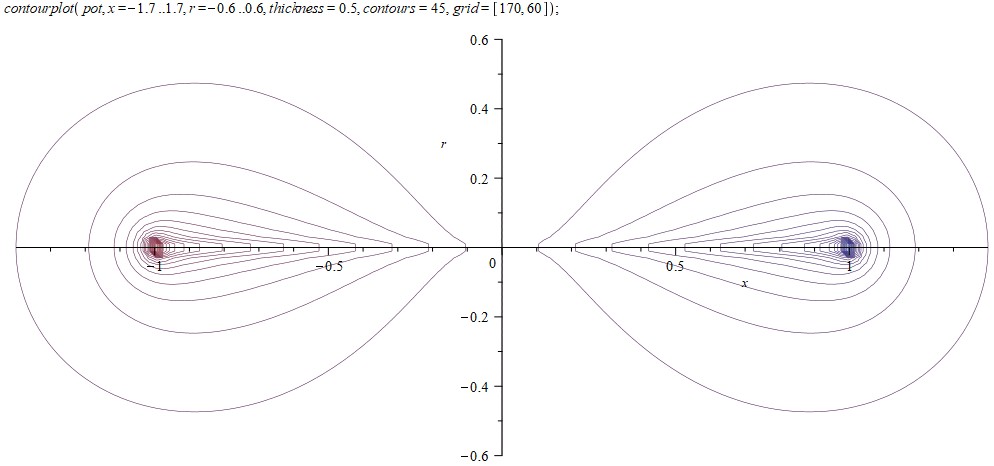
Как и в любых скрещенных электрических и магнитных полях, вокруг электрического заряда и магнитного монополя существуют потоки энергии, определяемые вектором Пойнтинга $$\vec{S}\sim\vec{E}\times\vec{B}$$. Они замкнуты и охватывают ось симметрии системы, что может означать наличие в ней момента импульса.

Если заряд движется строго на монополь, то взаимодействие между ними отсутствует. Действительно, монополь не испытывает действие электрического поля заряда. Магнитное поле заряда на линии движения нулевое. Монополь не создает электрическое поле, а его магнитное поле коллинеарно скорости заряда, поэтому силы на заряд тоже не действуют. Отсутствие взаимодействия в этом случае наводит на мысль о том, что момент импульса остается неизменным.

Есть и другое качественное рассуждение в пользу неизменности момента импульса. По соображениям размерности момент импульса, как безразмерная величина (в единицах c = ħ = 1), не может зависеть от расстояния между зарядом и монополем — единственного размерного параметра системы. Убедимся в этом непосредственным вычислением.

Поместим электрический заряд q в точку $$\vec{a}$$ и магнитный заряд m в точку $$-\vec{a}$$. Тогда они будут создавать поля

$$\vec{E}(\vec{R})={q\over |\vec{R}-\vec{a}|^3}(\vec{R}- \vec{a}),\quad\vec{B}(\vec{R}) ={m\over |\vec{R} + \vec{a}|^3}(\vec{R} + \vec{a}).$$

Плотность импульса связана с вектором Пойнтинга

$$\vec{P} = {\vec{S} \over c^2} = {1\over 4\pi c}\vec{E}\times\vec{B}= {qm\over 4\pi c}{(\vec{R}-\vec{a})\times (\vec{R}+\vec{a})\over \left(\left(R^2+a^2\right)^2-4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$

Полный момент импульса находится интегрированием по всему пространству

$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV={qm\over 2\pi c}\int\! dV{\vec{R}\times[\vec{R}\times\vec{a}]\over \left(\left(R^2 + a^2\right)^2- 4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$

Выбираем ось z вдоль $$\vec{a}$$, угол между этой осью и радиус-вектором $$\vec{R}$$ есть полярный угол θ. Из соображений симметрии момент импульса должен быть направлен по оси z (компонента, перпендикулярная оси z, при интегрировании по всему объему исчезает). Раскрываем двойное векторное произведение, находим проекцию на z и сразу интегрируем по азимутальному углу φ

$$L_z={qm\over c}\int\limits_0^{\infty}\! R^2dR\int\limits_{-1}^{1}\! d(\cos\theta){-a\,R^2\sin^2\theta\over \left(\left(R^2 + a^2\right)^2- 4(R\,a\cos\theta)^2\right)^{3/2}}.$$

Разделим числитель и знаменатель на a⁶ и введем новую безразмерную переменную интегрирования r = R/a. Таким образом, мы избавились от явной зависимости момента импульса от расстояний. Двойной интеграл не зависит от параметров задачи. С помощью любимого математического пакета можно убедиться, что он равен 1.

$$L_z=-{qm\over c}\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! d(\cos\theta){1-\cos^2\theta\over \left(\left(r^2 + 1\right)^2- 4r^2\cos^2\theta\right)^{3/2}}=-{qm\over c}.$$

Таким образом, момент импульса в системе заряда и монополя направлен к последнему и равен (с точностью до несущественного множителя c) произведению их величин.

В квантовой механике момент импульса квантуется. Из полуклассических соображений приравнивая полученное выше выражение для момента к минимальному значению ħ/2, мы получаем такое же ограничение на минимальные («элементарные») значения электрического и магнитного зарядов, как и в теории Дирака (где ограничение следует из дискретности прироста фазы волновой функции заряда при полном обороте вокруг монополя)

$$q_{min}\, m_{min}={\hbar c\over 2}.$$

Как видим, присутствие во Вселенной хотя бы одного монополя приводит к квантованию всех электрических зарядов.

В завершение потренируемся в технике вычисления интегралов. Обозначим искомый интеграл через $$I$$:

$$I=\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! dz{1-z^2\over \left(\left(r^2 + 1\right)^2- 4r^2z^2\right)^{3/2}}=\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! dz{1-z^2\over \left(\left(r^2 - 1\right)^2+4r^2- 4r^2z^2\right)^{3/2}}.$$

Рассмотрим вспомогательный интеграл $$J(b)$$, дополнительно зависящий от некоторого параметра $$b$$:

$$J(b)=\int\limits_{-1}^{1}{dz\over \sqrt{\left(r^2 - 1\right)^2+ 4b^2r^2\left(1-z^2\right)}}.$$

Вычислим $$J'(b)$$:

$$J'(b)=\int\limits_{-1}^{1}{dz\over \sqrt{\left(r^2 - 1\right)^2+ 4b^2r^2\left(1-z^2\right)}^3}\cdot\left(-{1\over 2}\right)8br^2\left(1-z^2\right).$$

$$J'(1)$$ с точностью до коэффициентов совпадает с внутренним интегралом в $$I$$. Сравнивая их, можем записать:

$$I=\int\limits_0^{\infty}\! r^2dr\cdot{-J'(1)\over 4}.$$

Упростим и вычислим $$J(b)$$, введя константы $$A=\left(r^2 - 1\right)^2$$ и $$B=4b^2r^2$$:

$$\begin{align*}&\int\limits_{-1}^{1}{dz\over \sqrt{A+B\left(1-z^2\right)}}={2\over\sqrt{B}}\int\limits_{0}^{1}{dz\over\sqrt{{A\over B}+1-z^2}}= \begin{vmatrix} z=\sqrt{{A\over B}+1}\sin\varphi\\ dz=\sqrt{{A\over B}+1}\cos\varphi\ d\varphi \\ \end{vmatrix}=\\ &={2\over\sqrt{B}}\int\limits_{0}^{\arcsin\left(1/\sqrt{{A\over B}+1}\right)}{\sqrt{{A\over B}+1}\cos\varphi\ d\varphi\over\sqrt{{A\over B}+1-\left({A\over B}+1\right)\sin^2\varphi}}= {2\over\sqrt{B}}\int\limits_{0}^{\arcsin\sqrt{B\over A+B}}d\varphi=\\ &={2\over\sqrt{B}}\arcsin\sqrt{B\over A+B}={2\over\sqrt{B}}\arctg\sqrt{B\over A}. \end{align*} $$

Возвращаемся к исходным переменным:

$$\begin{align*}J'(b)&={d\over db}\left({2\over\sqrt{4b^2r^2}}\arctg\sqrt{4b^2r^2\over \left(r^2 - 1\right)^2}\right)= {d\over db}\left({1\over br}\arctg{2br\over \left|r^2 - 1\right|}\right)=\\ &=-\frac{1}{b^2 r}\arctg\dfrac{2rb}{|r^2 - 1|} +\frac{1}{br \left(1+ \dfrac{4r^2 b^2}{|r^2 - 1|^2}\right)}{2r\over |r^2 - 1|}. \end{align*}$$

Подставляем $$b=1$$ и упрощаем:

$$\begin{align*}J'(1)&=-\frac{1}{r}\arctg\dfrac{2r}{|r^2 - 1|} +\frac{2|r^2 - 1|}{\left(r^2 - 1\right)^2+ {4r^2}}. \end{align*}$$

Возвращаемся к первоначальному интегралу, разбиваем на сумму интегралов на интервалах $$(0,1)$$ и $$(1,\infty)$$, чтобы раскрыть модули. Также выполняем замену переменных $$r=1/u$$ в первом из них и группируем в виде общего интеграла:

$$\begin{align*} I&=\int\limits_0^{\infty}\! dr\left(\frac{r}{4}\arctg\dfrac{2r}{|r^2 - 1|}-\frac{r^2|r^2 - 1|}{2\left(\left(r^2 - 1\right)^2+ {4r^2}\right)}\right)=\\ &=\int\limits_0^{1}\! dr\left(\frac{r}{4}\arctg\dfrac{2r}{1-r^2}-\frac{r^2(1-r^2)}{2\left(\left(r^2 - 1\right)^2+ {4r^2}\right)}\right)+\\ &\qquad\qquad+\int\limits_1^{\infty}\! dr\left(\frac{r}{4}\arctg\dfrac{2r}{r^2 - 1}-\frac{r^2(r^2 - 1)}{2\left(\left(r^2 - 1\right)^2+ {4r^2}\right)}\right)=\\ &=\int\limits_\infty^{1}\! -{du\over u^2}\left(\frac{1}{4u}\arctg\dfrac{2/u}{1-1/u^2}-\frac{(1/u)^2(1-1/u^2)}{2\left(\left(1/u^2 - 1\right)^2+ 4/u^2\right)}\right)+ \int\limits_1^{\infty} dr\ldots=\\ &=\int\limits_1^{\infty}\! {du\over u^4}\left(\frac{u}{4}\arctg\dfrac{2u}{u^2-1}-\frac{u^2(u^2-1)}{2\left(\left(1-u^2 \right)^2+ 4u^2\right)}\right)+ \int\limits_1^{\infty}\! dr\ldots=\\ &=\int\limits_1^{\infty}\! \left(1+{1\over r^4}\right)\left(\frac{r}{4}\arctg\dfrac{2r}{r^2 - 1}-\frac{r^2(r^2 - 1)}{2\left(\left(r^2 - 1\right)^2+ 4r^2\right)}\right)dr. \end{align*}$$

Теперь, чтобы избавиться от арктангенса, введем новую переменную $$\psi$$:

$$ \begin{tikzpicture}[domain=1.001:7,scale=0.5] \draw[very thin] (-0.1,-0.1) grid (7+0.1,2+0.1); \draw[->] (-0.2,0)--(7.6,0) node[right] {$r$}; \draw[->] (0,-0.2)--(0,2+0.6) node[right] {$\psi$}; \draw plot (\x,{atan(2*\x/(\x*\x-1))/180*3.14}) node[above right] {$\psi=\arctg\dfrac{2r}{r^2 - 1}$}; \end{tikzpicture} \begin{align*} &\!\!\!r^2-{2\over\tg\psi}r-1=0,\\ r&={1\over\tg\psi}+\sqrt{{1\over\tg^2\psi}+1}={1\over\tg\psi}+{1\over\sin\psi}={\cos\psi+1\over\sin\psi},\\ r^2&={(\cos\psi+1)^2\over1-\cos^2\psi}={\cos\psi+1\over1-\cos\psi},\\ r^2-1&={\cos\psi+1-1+\cos\psi\over1-\cos\psi}={2\cos\psi\over1-\cos\psi},\\ dr&={-\sin^2\psi-\cos\psi(\cos\psi+1)\over\sin^2\psi}d\psi=-{d\psi\over 1-\cos\psi} . \end{align*} $$

Из скетча и выражения для производной видно, что замена монотонная. При решении квадратного уравнения был выбран корень с плюсом, так как мы работаем в области $$r>1$$.

$$\begin{align*}I&=\int\limits_{\pi/2}^{0} \left(1+{(1-\cos\psi)^2\over (\cos\psi+1)^2}\right)\left(\frac{\cos\psi+1}{4\sin\psi}\psi-\frac{\frac{\cos\psi+1}{1-\cos\psi}\frac{2\cos\psi}{1-\cos\psi}}{2\left(\left(\frac{2\cos\psi}{1-\cos\psi}\right)^2+ 4\frac{\cos\psi+1}{1-\cos\psi}\right)}\right){-d\psi\over 1-\cos\psi}=\\ &=\int\limits_{0}^{\pi/2} {2+2\cos^2\psi\over (\cos\psi+1)^2}\left(\frac{\cos\psi+1}{4\sin\psi}\psi-\frac{(\cos\psi+1)\cos\psi}{4\cos^2\psi+ 4({\cos\psi+1})({1-\cos\psi})}\right){d\psi\over 1-\cos\psi}=\\ &=\int\limits_{0}^{\pi/2} {1+\cos^2\psi\over \cos\psi+1}\left(\frac{1}{2\sin\psi}\psi-\frac{\cos\psi}{2\left(\cos^2\psi+ 1-\cos^2\psi\right)}\right){d\psi\over 1-\cos\psi}=\\ &={1\over 2}\int\limits_{0}^{\pi/2} {1+\cos^2\psi\over 1-\cos^2\psi}\left(\frac{\psi}{\sin\psi}-\cos\psi\right)d\psi= {1\over 2}\int\limits_{0}^{\pi/2} {1+\cos^2\psi\over \sin^2\psi}\left(\frac{\psi}{\sin\psi}-\cos\psi\right)d\psi=\\ &={1\over 2}(I_1-I_2)\Bigg|_0^{\pi/2}. \end{align*} $$

Найдем каждый из неопределенных интегралов $$I_1$$ и $$I_2$$ по отдельности. Первый интеграл:

$$\begin{align*} I_1=\int {1+\cos^2\psi\over \sin^2\psi}\frac{\psi}{\sin\psi}\,d\psi= \int {1+\cos^2\psi\over \sin^4\psi}\,\psi\,{\sin\psi}\,d\psi= \int {1+\cos^2\psi\over (1-\cos^2\psi)^2}\,\psi\,d(-\cos\psi). \end{align*} $$

Для интегрирования по частям сначала разложим дробь на простейшие:

$$\begin{align*} {1+x^2\over (1-x^2)^2}&={A\over 1-x}+{B\over (1-x)^2}+{C\over 1+x}+{D\over (1+x)^2}=\\ &={A(1-x)(1+x)^2+B(1+x)^2+C(1+x)(1-x)^2+D(1-x)^2\over (1-x^2)^2}. \end{align*}$$

Если приравнять числители и подставить $$x=1$$, получим $$B=1/2$$. При подстановке $$x=-1$$ получаем $$D=1/2$$. Так как $$B(1+x)^2+D(1-x)^2$$ уже дает $$1+x^2$$, $$A=C=0$$.

$$ \int\!{1+x^2\over (1-x^2)^2}\,dx=\int\!{dx\over 2(1-x)^2}+\int\!{dx\over 2(1+x)^2}={1\over 2(1-x)}-{1\over 2(1+x)}+C={x\over 1-x^2}+C. $$

$$\begin{align*} I_1=-\psi{\cos\psi\over 1-\cos^2\psi} +\int {\cos\psi\over 1-\cos^2\psi}d\psi=-\psi{\cos\psi\over \sin^2\psi}-{1\over\sin\psi}+C. \end{align*} $$

Второй интеграл:

$$\begin{align*} I_2=\int {1+\cos^2\psi\over \sin^2\psi}\cos\psi\ d\psi= \int {2-\sin^2\psi\over \sin^2\psi}\ d(\sin\psi)=-{2\over\sin\psi}-\sin\psi+C. \\ \end{align*} $$

Наконец, получаем численное значение искомого интеграла:

$$\begin{align*}I&={1\over 2}(I_1-I_2)\Bigg|_0^{\pi/2}={1\over 2}\left(-\psi{\cos\psi\over \sin^2\psi}-{1\over\sin\psi}+{2\over\sin\psi}+\sin\psi\right)\Bigg|_0^{\pi/2}=\\ &={1\over 2}\left({\sin\psi-\psi\cos\psi\over \sin^2\psi}+\sin\psi\right)\Bigg|_0^{\pi/2}= 1-{1\over 2}\lim_{\psi\to0}{\sin\psi-\psi\cos\psi\over \sin^2\psi}=\\ &=1-{1\over 2}\lim_{\psi\to0}{\psi+o(\psi^2)-\psi+o(\psi^2)\over \psi^2+o(\psi^2)}=1. \end{align*}$$