Скрытый импульс
Недавно на гиктаймсе писали про невозможный двигатель на электромагнитной тяге. Для появления такой тяги физических оснований нет, обсуждать его мы не будем. А вот в комментариях завязалась интересная дискуссия о том, может ли замкнутая покоящаяся система изменить свой электромагнитный импульс и за счет отдачи прийти в состояние макроскопического движения. Краткий ответ — нет. Развернутый ответ — ниже.
Введение
Ранее мы рассматривали потоки электромагнитной энергии в постоянных электрических и магнитных полях. Эти потоки были замкнутыми. Однако можно составить такую систему неподвижных источников электрического и магнитного полей, в которой потоки энергии не замкнуты. Следовательно, такие системы обладают ненулевым суммарным электромагнитным импульсом.
Пример такой системы — тороидальный магнит внутри цилиндрического конденсатора. Покажем, что в ней запасается ненулевой электромагнитный импульс.
$$\begin{tikzpicture}[line width=0.21mm,scale=1.898] \coordinate (A) at (1.7,2.3); \draw[dashed,color=gray] (1.9,0.7) arc (-80:80:-0.2 and 0.8) (2.25,0.9) arc (-150:150:-0.5 and 1.2);%torus \draw[thin,dashed,color=gray] (0,1.5) ellipse (0.146 and 0.6) ++(0,-0.6) -- +(1.4,0) +(1.8,0) -- +(4,0) ++(0,1.2) -- +(1.4,0) +(1.8,0) -- +(4,0); \draw (4,1.5) ellipse (0.146 and 0.6) node {$-$} ++(0,-0.6) -- +(-0.45,0) ++(0,1.2) -- +(-0.45,0); \draw[thin,dashed,color=gray] (0,0) arc (-90:90:0.5 and 1.5);%l.ell \draw (4,0) -- (0,0) arc (270:90:0.5 and 1.5) -- +(4,0); \draw (4,1.5) ellipse (0.5 and 1.5);%r.ell \draw (-0.8,1.5) node {$+$}; \draw[thin,->] (A) -- +(0.6,0) node[right] {$\vec{S}$}; \draw[thin,->] (A) -- +(0.4,0.5) node[right] {$\vec{B}$}; \draw[thin,->] (A) -- +(0.15,-0.6) node[right] {$\vec{E}$}; \draw[opacity=0] (-0.9,0) rectangle (4.5,3); \end{tikzpicture}$$
Внутри магнита электрическое поле направлено по радиальным линиям, магнитное — по концентрическим окружностям, а вектор Пойнтинга $$\vec{S}\sim\vec{E}\times\vec{B}$$ — вдоль оси конденсатора. Снаружи соленоида нет магнитного поля и потоков энергии. Поэтому суммарный электромагнитный импульс в такой системе направлен вдоль оси симметрии.
На первый взгляд ненулевой импульс у внешне покоящейся системы выглядит крайне странно и приводит к парадоксам. Например, при изменении тока через соленоид изменяется импульс электромагнитного поля. Система получает механический импульс отдачи и начинает перемещаться. После закачки энергии в сверхпроводящий соленоид замкнутая система без взаимодействия со внешними телами перемещается в произвольном направлении на произвольное расстояние?! Это более чем странно.
Из специальной теории относительности следует, что импульс замкнутой системы относительно центра масс равен нулю (теорема о центре масс). Следовательно, электромагнитный импульс компенсируется импульсом другой природы. Его называют «скрытым импульсом».
Впервые понятие скрытого импульса ввели Шокли и Джеймс в 1967 году. Сведения о скрытом импульсе в доступной форме систематизированы в статье «Hidden momentum, field momentum, and electromagnetic impulse» (David Babson, Stephen P. Reynolds, Robin Bjorkquist and David J. Griffiths).
Сначала докажем теорему о центре масс. Затем выведем величину скрытого импульса модельной системы, которая встречается у Шокли и Джеймса. Также объясним природу скрытого импульса в различных системах. В завершение рассмотрим основные ошибки критиков скрытого импульса.
Ниже мы употребляем понятия «импульс» и «поток энергии» как синонимы. В специальной теории относительности эти величины пропорциональны с коэффициентом $$c^2$$, так как связаны с компонентами симметричного тензора
Теорема о центре масс
Докажем, что суммарный импульс замкнутой системы относительно ее центра масс равен нулю. Мы используем тензорные обозначения четырехмерных величин.
Координаты $$X^i$$ центра масс (точнее, центра энергии):
$$X^i=\cfrac{\int x^i\,T^{00}\,d^3x}{\int T^{00}\,d^3x},$$
где плотность энергии $$T^{00}$$ определяется временной компонентой тензора
По условию теоремы координаты центра энергии не меняются со временем. Продифференцируем их по времени и приравняем к нулю:
$$\int x^i\,{\partial T^{00}\over\partial x^0}\,d^3x}=0.$$
Воспользуемся законом сохранения энергии $$\partial_\mu T^{\mu\nu}=0$$ и перепишем подынтегральное выражение:
$$x^i\,\partial_0 T^{00}=-x^i\,\partial_j T^{j0}=-\partial_j(x^iT^{j0})+T^{j0}\,\partial_j x^i=-\partial_j(x^iT^{j0})+T^{i0}.$$
Интеграл от первого слагаемого как от дивергенции приводится с помощью теоремы Гаусса к интегралу по бесконечно удаленной поверхности от нулевой (на бесконечности) функции. В итоге мы получили, что интеграл от плотности потока энергии $$T^{i0}$$ с необходимостью нулевой. Таким образом, полный поток энергии относительно центра масс системы равен 0.
Cкрытый импульс в модельной системе
Рассмотрим виток с током в однородном электрическом поле. В такой системе тоже есть ненулевой момент импульса электромагнитного поля.
Чтобы выявить природу компенсирующего скрытого импульса, применим модель витка с током постоянного сечения S, в которой носители заряда движутся свободно, без сопротивления.
$$\dvisvgm \usetikzlibrary{animations} \newcommand{\mycharge}[1][]{ \fill[red!80] (#1) circle (0.59mm); \draw[white,line width=0.21mm] (#1) +(-1pt,0) -- +(1pt,0) +(0,-1pt) -- +(0,1pt); } \begin{tikzpicture}[join=round,scale=2.109,>=stealth] \draw[opacity=0,line width=0.2mm, use as bounding box] (-0.3,-0.32) rectangle (2.74,2); \def\w{0.08} \def\ww{1.92} \def\p{0.1} \draw (2.5,0.5)--++(0,1) [->] node[right] {$\vv{E}$}; \draw (-\p,\w)--(-\p,\ww) [<->,draw=gray] node[midway,left] {$h$}; \draw (\w,-\p)--(\ww,-\p) [<->,draw=gray] node[midway,below] {$l$}; \draw[rounded corners=1,line width=3.15mm,draw=brown!34](\w,\w) node[above right] {$A$}--(\ww,\w) node[above left] {$D$}--(\ww,\ww)node[below left] {$C$}--(\w,\ww)node[below right]{$B$}--cycle; \pgfmathsetmacro\sta{(\ww-\w)/6} \pgfmathsetmacro\stb{(\ww-\w)/3} \begin{scope} :xshift= {0s="0",3s="-\sta cm",repeats} \foreach \x in {0,1,...,5} \mycharge[\ww-\sta*\x,\w]; \end{scope} \begin{scope} :xshift= {0s="0",3s="\stb cm",repeats} \foreach \x in {0,1,2} \mycharge[\w+\stb*\x,\ww]; \end{scope} \pgfmathsetmacro\stc{1/4} \def\xval#1{(\ww-\w)/1.5*((#1)*(#1)*0.5+#1)+\w} \foreach \n in {0,\stc,...,0.999} { \pgfmathsetmacro\xa{\xval{\n}} \pgfmathsetmacro\xb{\xval{\n+\stc}} \pgfmathsetmacro\y{\xb-\xa} \begin{scope} :yshift={0s="0",3s="\y cm",repeats} \mycharge[\w,\xa]; \end{scope} \begin{scope} :yshift={0s="0",3s="-\y cm",repeats} \mycharge[\ww,\xb]; \end{scope} } \draw (1.2,0.25)--++(-0.4,0) [->] node[midway,above] {$\vv{v}_1$}; \draw (0.55,1.75)--++(0.9,0) [->] node[midway,below] {$\vv{v}_2$}; \end{tikzpicture}$$
Пусть в точке A носители заряда имеют скорость $$v_1$$. На участке AB за счет работы электрического поля их скорость растет до величины $$v_2$$. Одновременно с этим снижается плотность носителей заряда, чтобы величина тока $$I=jS=qnvS$$ оставалась постоянной: $$n_1v_1=n_2v_2$$. Далее носители движутся с постоянной скоростью до точки C, замедляются до $$v_1$$ к точке D и возвращаются на этой скорости в точку A.
В нерелятивистском случае, когда импульс одного носителя заряда есть $$p=mv$$, полный импульс носителей на участках BC и AD равен
$$P_\text{нерел}=mv_2n_2Sl-mv_1n_1Sl=0.$$
Но если учесть релятивистские эффекты, когда $$p=\gamma mv$$,
$$P_\text{рел}=\gamma_2mv_2n_2Sl-\gamma_1mv_1n_1Sl=(\gamma_2-\gamma_1){mIl\over q}.$$
Разность кинетической энергии $$K=\gamma mc^2$$ носителей на этих участках определяется работой электрического поля:
$$\gamma_2 mc^2-\gamma_1 mc^2=qEh.$$
Таким образом,
$$P_\text{скр}={IlEh\over c^2}={\mu E\over c^2},$$
где $$\mu$$ — магнитный момент витка с током.
Результат легко обобщается на случай произвольного точечного магнитного диполя в неоднородных электрических полях. Электрическое поле, перпендикулярное плоскости витка, не влияет на движение зарядов. Переходя от проекции электрического поля на плоскость витка к вектору, получаем
$$\vec{P}_\text{скр}={1\over c^2}\,\vec\mu\times\vec{E}.$$
Можно показать, что электромагнитный импульс в системе из заряда q и диполя $$\mu$$ определяется формулой
$$\vec{P}_\text{эм}=-{1\over c^2}\vec\mu\times\vec{E},$$
где $$\vec{E}=q\vec{R}/R^3$$ — электрическое поле заряда в точке, где находится диполь. Электромагнитный импульс полностью компенсируется скрытым импульсом. Мы не будем делать расчет конкретно для этой системы. Вместо этого покажем, что такая компенсация происходит всегда.
Скрытый импульс и импульс электромагнитного поля
В произвольном электростатическом поле с потенциалом $$\varphi$$ выражение для скрытого импульса витка с током I приобретает вид
$$\vec{P}_\text{скр}=-{I\over c^2}\oint\varphi\,d\vec{l}.$$
Если задана объемная плотность тока $$\vec{j}$$, то
$$\vec{P}_\text{скр}=-{1\over c^2}\int\varphi\vec{j}\,dV.$$
Подставим в последнюю формулу уравнение Максвелла для стационарных полей $$\nabla\times\vec{B}=(4\pi/c)\vec{j}$$:
$$\begin{align*} \vec{P}_\text{скр}&=-{1\over 4\pi c}\int\varphi\,\nabla\times\vec{B}\,dV=-{1\over 4\pi c}\int\left(\nabla\times\varphi\vec{B}-\nabla\varphi\times\vec{B}\right)\,dV=\\ &={1\over 4\pi c}\oint\varphi\vec{B}\times d\vec{S}-{1\over 4\pi c}\int\vec{E}\times\vec{B}\,dV=-{1\over c^2}\int\vec{S}\,dV=-\vec{P}_\text{эм}. \end{align*}$$
Первое слагаемое — интеграл по бесконечно удаленной поверхности — для замкнутых ограниченных в пространстве систем равен 0. Таким образом, мы получили, что ненулевой полный электромагнитный импульс системы всегда компенсируется скрытым импульсом. Полный импульс покоящейся стационарной системы — нулевой.
Природа скрытого импульса
Скрытый импульс связан с механическим движением носителей зарядов. Масса носителей фигурировала в выводе, но сократилась в итоговом ответе.
Скрытый импульс имеет релятивистский характер. Если бы не поправки специальной теории относительности, скрытый импульс был бы нулевым.
Природа скрытого импульса зависит от самой системы. В рассмотренной выше модели скрытый импульс (и поток энергии) связан с ускорением зарядов. В модели тока заряженной несжимаемой жидкости скрытый поток энергии вызывается перепадом давления. Во вращающемся заряженном диэлектрике (например, в сфере) импульс и поток энергии запасен в движении участков с разным механическим напряжением.
$$\begin{tikzpicture}[scale=2.109,line width=0.21mm,draw=red,node distance=4cm] \draw [fill=red!10] circle (0.7); \draw (-120:.15) [->,thin,black] arc(240:-60:.15); \def\n{12} \foreach \s in {1,...,\n} \node at ({360/\n * (\s-1)}:0.6) {$+$}; \node[fill=red!10,draw,circle] at (0,-1.3) {$+$}; \draw (0,-0.844) node {$\text{растянуто}$}; \draw (0,0.82) node {$\text{сжато}$}; \draw[line width=5,draw=black!20] (2,-0.3)+(0,-0.5) arc (270:90:0.5) -- +(2,0) node[midway,above=0.05mm] {$\text{натяжение меньше}$} arc (90:-90:0.5) -- +(-2,0) node[midway,below=-0.1mm] {$\text{натяжение больше}$}; \draw[fill=green!10,draw=green!40!black] (2,-0.3) circle(0.46) +(2,0) circle(0.46); \draw (2,-0.3) +(-120:.1) [->,thin,black] arc(240:-60:.1); \end{tikzpicture}$$
Поток механической энергии в последнем случае аналогичен потоку энергии в ременной передаче. Нижняя половина ремня на рисунке справа перемещается от нагрузки к двигателю. Она натянута больше, чем верхняя. При этом поток механической энергии направлен к нагрузке.
В настоящих электромагнитах скрытого импульса нет
В примере из введения нельзя заменить тороидальный магнит на соленоид с током. Если намотать соленоид металлическим проводом, то ни скрытого импульса внутри него, ни электромагнитного импульса снаружи не будет.
Всё дело в экранировке внешнего электрического поля в металле. Перераспределение поверхностных зарядов приводит к тому, что поверхность идеального проводника становится эквипотенциальной, и интеграл от плотности скрытого импульса $$-\varphi\vec{j}$$ зануляется.
Также исчезает и электромагнитный импульс. Электрическое поле перпендикулярно эквипотенциальным поверхностям, а вектор Пойнтинга направлен по касательным к ним. Потоки энергии текут вдоль эквипотенциальных поверхностей и вынуждены быть замкнутыми.
Ненулевое сопротивление настоящих металлов приводит к падению потенциала вдоль проводника и попаданию части потока энергии внутрь. Энергия исходит из источника тока и перемещается к проводнику, в котором переходит в тепло. Такая система уже нестационарна. В ней энергия перемещается от одной части к другой, и полный импульс отличен от нуля.
Чтобы в системе появился и электромагнитный, и скрытый импульс, вместо электромагнита надо взять неметаллический источник магнитного поля. Скрытый импульс $$-\varphi\vec{j}$$ будет запасен в молекулярных токах Ампера.
Критика скрытого импульса
Понятие скрытого импульса часто подвергается критике недостаточно компетентными авторами. Рассмотрим распространенные ошибки критиков на примере текста некоего Джеррольда Франклина.
-
В статье рассуждения начинаются не с вектора Пойнтигна, выражение для которого выводится из принципа наименьшего действия, а с применения третьего закона Ньютона к силе Лоренца. Начиная не с общих формул, а с частных, нельзя прийти к общим выводам.
-
Утверждается, что теорему о центре масс нельзя применить к электромагнитному полю, потому что взаимодействие с веществом $$-\vec{j}\cdot\vec{E}$$ нарушает равенство $$\partial_\mu T^{\mu\nu}_\text{эм}=0$$. Но правильно применять теорему к полной системе, включающей и электромагнитное поле, и вещество, а не к ее части.
-
Автор критикует модель витка с током, заявляя, что в ней появятся поверхностные заряды, компенсирующие внешнее электрическое поле. Аргумент имеет смысл только для систем с точной компенсацией зарядов разного знака вроде металлических проводников. Его легко обойти, потребовав, чтобы все заряды в витке были одного знака.
-
Еще одна грубая ошибка присутствует в предложении, по которому перераспределение зарядов по поверхности металлического проводника не приводит к исчезновению электромагнитного импульса. Суммарный ненулевой электромагнитный импульс присутствует в системе с ненулевым суммарным потоком электромагнитной энергии. Он появляется в системе с источниками и стоками энергии $$-\vec{j}\cdot\vec{E}\ne 0$$. Внутри и снаружи идеального проводника $$\vec{j}\cdot\vec{E}=0$$, электрическое поле существенно искажается и суммарный электромагнитный поток энергии исчезает.
-
Неверный логический переход в следующем выводе: во вращающихся диэлектрических заряженных телах не может быть ускорения носителей зарядов и связанной релятивистской добавки, и поэтому в ней нет скрытого импульса. На самом деле скрытый импульс есть, он имеет другую природу и связан с механическим напряжением, как мы показали выше.
Автору не удалось показать ни неприменимость теоремы о центре масс, ни отсутствие необходимости во введении понятия скрытого импульса, ни отсутствие самого скрытого импульса.
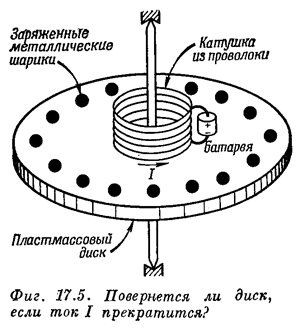
Комментарии
Электрического поля внутри заряженного цилиндра нет. Значит, скрытый импульс будет нулевым (что вполне естественно, потому что скрытый импульс компенсирует электромагнитный импульс). Поэтому логично поставить под сомнение утверждение, что вихревое электрическое поле сдвинет цилиндр. В разных областях цилиндра проекция поля на поверхность будет направлена в противоположные стороны. Скорее всего суммарный эффект будет нулевым.
Вообще уравнения Максвелла подразумевают сохранение энергии и импульса:
Так что во всех мыслимых электромагнитных эффектах суммарный импульс поля и вещества всегда будет сохраняться.
Возмем заряженный цилиндрический конденсатор и пропустим вдоль его оси металический проводник с током. Электромагнитный импульс в зазоре коденсатора очевидно есть
(магнитное поле тока + электрическое поле конденсатора перпендикулярные друг другу создают электромагнитный ипульс вдоль оси конденсатора).
1. Допустим скрытый импульс в данной системе существует. Тогда при разряде конденсатора через пространство между обкладками возникнет сила Лоренца, которая превратит
электромагнитный импульс в механический. Как Вы утверждали ранее, в неподвижной системе электромагнитный импульс равен скрытому и суммарный импульс нулевой. Откуда появился механический импульс?
2 Допустим скрытого импульса нет. Отключим ток — система останется в покое. Куда делся электромагнитный импульс?
Чтобы точно ответить на вопрос, что происходит с электромагнитным импульсом, нужно разобраться с граничными условиями. Дело в том, что бесконечный провод с током и бесконечный цилиндрический конденсатор несут в себе бесконечно большую энергию. И в таких системах можно получить любое противоречие. Реальные системы ограничены в пространстве. И то, что происходит на границе, влияет на ответ.
Реальный проводник с током должен быть замкнут. В зависимости от того, как это будет сделано, скрытый импульс может присутствовать или нет. Можно рассмотреть два варианта.
В первом варианте замкнем центральную жилу в кольцо и предположим, что она из сверхпроводника. Тогда источник тока не нужен. Суммарный электромагнитный импульс будет нулевой, так как поток энергии будет замкнутым внутри кольца из коаксиального кабеля. Скрытый импульс нулевой, так как нет движения зарядов в перепаде потенциала.
Во втором варианте рассмотрим подключение через коаксиальный кабель лампочки к батарейке. В этой системе есть ненулевой поток энергии (а значит и импульс) от батарейки к лампочке. Это нестационарная система, в которой центр масс действительно перемещается (батарейка становится легче по формуле $$E=m_0c^2$$, а лампочка — тяжелее, если пренебрегать потерей на излучение). И по закону сохранения импульса при остановке тока этот электромагнитный импульс перейдет в механический. Как показывает вычисление, импульс, связанный с перемещением центра масс, совпадает с электромагнитным импульсом. Это значит, что скрытого импульса в этой системе тоже не будет. Правда, мы получили противоречие с выражением для скрытого импульса $$-\varphi\vec{j}$$. Видимо, оно нуждается в уточнении для случая электрических полей неэлектростатической природы. Я обдумаю еще этот момент.
1. Заряжаем конденсатор.
2. Включаем ток в витке.
3. Разряжаем конденсатор.
4. Выключаем ток в витке.
При выполнении пункта 3 сила Лоренца раскручивает систему. В остальных пунктах механическое состояние системы не меняется.
Единственно избежать подобного «безобразия» — это предположить, что в пункте 2 момент импульса, передаваемый системе, равен передаваемому в пункте 3 с обратным знаком.
Это может быть, если скрытый импульс содержится в токе и равен, как раз $$-\varphi\vec{j}$$.
Из такого предположения следует, что может существовать сила электромагнитной природы, действующая вдоль тока — электродинамика Максвелла это отрицает.
Так что с электродинамикой Максвелла тут полный порядок :)
Оставьте свой комментарий