Парадокс Фейнмана, или потоки энергии в постоянных электромагнитных полях

В фейнмановских лекциях по физике (выпуск 6, глава 17) есть описание следующего парадокса.

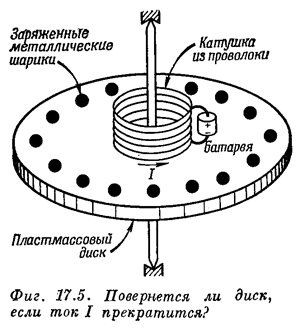
Представим, что мы конструируем прибор, в котором имеется тонкий круглый пластмассовый диск, укрепленный концентрически на оси с хорошими подшипниками, так что он совершенно свободно вращается. На диске имеется катушка из проволоки — короткий соленоид, концентричный по отношению к оси вращения. Через этот соленоид проходит постоянный ток I от маленькой батареи, также укрепленной на диске. Вблизи края диска по окружности на равном расстоянии размещены маленькие металлические шарики, изолированные друг от друга и от соленоида пластмассовым материалом диска. Каждый из этих проводящих шариков заряжен одинаковым зарядом Q. Вся картина стационарна, и диск неподвижен.

Предположим, что случайно, а может и намеренно, ток в соленоиде прекратился, но, разумеется, без какого-либо вмешательства извне. Пока через соленоид шел ток, более или менее параллельно оси диска проходил магнитный поток. После того как ток прервался, поток этот должен уменьшиться до нуля. Поэтому должно возникать индуцированное электрическое поле, которое будет циркулировать по окружностям с центром на оси диска. Заряженные шарики на периферии диска будут все испытывать действие электрического поля, касательного к внешней окружности диска. Эта электрическая сила направлена для всех зарядов одинаково и, следовательно, вызовет у диска вращающий момент. Из этих соображений можно ожидать, что, когда ток в соленоиде исчезнет, диск начнет вращаться. Если нам известны момент инерции диска, ток в соленоиде и заряд шариков, то можно вычислить результирующую угловую скорость.

Но можно рассуждать и по-другому. Используя закон сохранения момента количества движения, мы могли бы сказать, что момент диска со всеми его пристройками вначале равен нулю, поэтому момент всей системы должен оставаться нулевым. Никакого вращения при остановке тока быть не должно. Какое из доказательств правильно? Повернется ли диск или нет? Мы предлагаем вам подумать над этим вопросом.

Решение парадокса заключается в том, что в присутствии электрических и магнитных полей имеются потоки энергии, описываемые вектором Пойнтинга $$\vec{S} \sim \vec{E} \times \vec{B}$$. В предложенной Фейнманом конфигурации эти потоки замкнуты. Поскольку поток энергии однозначно связан с плотностью импульса, наличие замкнутых потоков энергии свидетельствует о присутствии ненулевого момента импульса. Таким образом, в системе изначально был запас момента импульса, который после исчезновения магнитного поля был передан диску.

Однако есть люди, которые убеждены в том, что выражение для вектора потока энергии через векторное произведение полей годится только для переменных электромагнитных полей (действительно, перенос энергии в этом случае можно увидеть непосредственно). Им не нравится, что, согласно выражению для вектора Пойнтинга, энергия течет от источника постоянного тока к нагрузке не «по проводам», а снаружи. Основной аргумент сводится к тому, что на поток энергии легко влияют манипуляции с проводом, наличие примесей, разрывов; в то время как никакими телами снаружи, например, дополнительными зарядами или магнитами, остановить поток энергии к нагрузке не удается.

Противники применения вектора Пойнтинга в статике придумывают в этом случае другие выражения для плотности энергии, например, $$\varphi \vec{j}$$. Но такое выражение тоже не лишено недостатков, приписываемых вектору Пойнтинга. Даже если отбросить требование единообразного описания явлений и попытаться применить для зарядов и катушки выражение $$\varphi \vec{j}$$, мы сразу столкнемся с тем, что потенциал φ в точках катушки (а, значит, и и момент импульса системы) легко изменить, поместив систему внутрь большого проводящего заряженного ящика и меняя его заряд. Это плохо согласуется с гипотезой, по которой энергия, как и ток, течет по катушке.

В связи с такой критикой вектора Пойнтинга можно заняться интересным упражнением — непосредственно вычислить момент импульса электромагнитного поля через вектор Пойнтинга и сравнить его с моментом импульса, передаваемым диску. Даже если критиков эти вычисления не убедят, мы еще раз увидим красоту теории.

$$\dvisvgm \usepgflibrary{shadings} \begin{tikzpicture}[x=(-30:3cm),y=(30:3cm),z=(90:3cm),>=stealth] \def\R{1} \shade[ball color=orange,yscale=1.73,opacity=0.5] (0,0) circle (\R); \draw[blue,->] (0,0,0) -- (0,0,0.3\R) node[right] {$\vec{\mathfrak{m}}$}; \draw[thin] (0,0,0) -- (.7\R,.7\R,0) node[below,pos=0.5] {$a$}; \node[orange!80!black] at (0,\R,0.5*\R) {$Q$}; \def\r{0.075} \draw[blue,->,thick] (\r,0,0) arc (0:360:\r); \end{tikzpicture} $$

Для упрощения вычислений изменим систему, предложенную Фейнманом. Будем рассматривать не заряды на краю диска, а равномерно заряженную сферу радиуса a, в центре которой находится небольшая катушка, обладающая магнитным моментом $$\vec{\mathfrak{m}}$$. Магнитный момент, находящийся в начале координат, создает в точке $$\vec{R}$$ векторный потенциал

$$\vec{A} = {\vec{\mathfrak{m}} \times \vec{R} \over R^3}$$(1)

и магнитное поле

$$\vec{H} = {3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n})-\vec{\mathfrak{m}} \over R^3}, \quad \vec{n} = {\vec{R}\over R}.$$

$$\usetikzlibrary{arrows.meta,positioning,decorations.markings,backgrounds} \colorlet{EcolFL}{orange!80!black} \tikzset{EFieldLineArrow/.style={EcolFL,decoration={markings,mark=at position 1 with {\arrow{Stealth}}},postaction={decorate}}} \def\R{0.8} \def\NE{8} \begin{tikzpicture}[-,scale=6] \foreach \i [evaluate={\angle=(\i-1)*360/\NE;}] in {1,...,\NE}{ \draw[EFieldLineArrow] (\angle:0) -- (\angle:\R); } \node[draw=EcolFL,fill=white,circle, minimum size=4cm, inner sep=0, outer sep=0] (circ) at (0,0) {}; \node[EcolFL,right] at (0.56,0.56) {$\vec{E}$} \node[blue,right] at (0.59,0.2) {$\vec{H}$} \node[right] at (0.32,0.32) {$\otimes\vec{S}$} \node[above] at (0.72,0) {$\otimes\vec{S}$} \node[right] at (0.32,-0.3) {$\otimes\vec{S}$} \node[right] at (-0.48,0.32) {$\odot\vec{S}$} \node[above] at (-0.72,0) {$\odot\vec{S}$} \node[right] at (-0.48,-0.3) {$\odot\vec{S}$} \draw [-{Latex}, blue] (0,0) -- (0,.15) node [right] {$\vec{\mathfrak{m}}$}; \begin{scope}[scale=0.3,on background layer] \foreach \a [count=\b] in {1.2}{ \draw[blue,domain=0:6.28,samples=150, line width=0.1mm, decoration={markings,% mark=at position 0.1 with {\arrowreversed{Stealth}}, mark=at position 0.4 with {\arrow{Stealth}}, mark=at position 0.5 with {\arrow{Stealth}}, mark=at position 0.6 with {\arrow{Stealth}}, mark=at position 0.9 with {\arrowreversed{Stealth}}, mark=at position 1 with {\arrowreversed{Stealth}},}, postaction=decorate] plot (xy polar cs:angle=\x r,radius={\a+\b*cos(2*\x r)}); } \end{scope} \end{tikzpicture}$$

Вектор Поинтинга есть

$$\vec{S} = {c\over 4\pi}\vec{E}\times\vec{H}.$$(2)

Он связан с плотностью импульса

$$\vec{P} = {\vec{S} \over c^2}.$$(3)

Тогда, собирая вместе, получаем

$$\vec{P} = {1\over 4\pi c}{Q \over R^2} {1 \over R^3}\left[ \vec{n}\times \left(3\vec{n}\,(\vec{\mathfrak{m}} \cdot \vec{n}) -\vec{\mathfrak{m}} \right) \right] = {Q\over 4\pi c R^5}\left[\vec{\mathfrak{m}} \times \vec{n}\right].$$

Момент импульса

$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV=\int\! R\,{Q\over 4\pi c R^5}\,\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]dV.$$(4)

Введем сферические координаты так, что $$\vec{\mathfrak{m}}$$ направлен вдоль оси z, а угол θ есть угол между осью z и направлением $$\vec{R}$$. Тогда

$$\vec{L}=\int\limits_a^{\infty}\!{Q\over 4\pi c R^4}R^2dR \int\!\vec{n}\times\left[\vec{\mathfrak{m}} \times \vec{n}\right]d(\cos \theta)\,d\varphi.$$(5)

Первый интеграл берется элементарно. Второй есть усреднение двойного векторного произведения по всем направлениям $$\vec{n}$$, он кроме как от $$\vec{\mathfrak{m}}$$ ни от чего не зависит. Учитывая линейность интегрирования и векторного произведения, зависимость должна быть прямой пропорциональностью. Действительно, вычисления показывают, что второй интеграл равен

$$\vec{\mathfrak{m}}\int\!\sin^2\theta\,d(\cos \theta)\,d\varphi={8\pi\vec{\mathfrak{m}}\over 3}.$$

Окончательно получаем

$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$

Теперь посмотрим, какой момент импульса будет передан сфере после исчезновения магнитного поля. Начнем с момента электрических сил

$$\vec{M}=\int\!\vec{R}\times\rho\vec{E}\,dV={Q\over 4\pi}\int\!\vec{R}\times\vec{E}\,d(\cos\theta)\,d\varphi.$$

Учитывая, что вихревое электрическое поле определяется формулой

$$\vec{E}=-{1\over c}{\partial \vec{A}\over\partial t},$$

для момента импульса имеем

$$\vec{L}=\int\!\vec{M}\,dt={Q\over 4\pi c}\int\!d(\cos\theta)\,d\varphi\,\vec{R}\times\!\int\!-{\partial \vec{A}\over\partial t}dt.$$

Векторный потенциал уменьшается от начального значения $$\vec{A}$$, задаваемого формулой (1), до нуля. Поэтому последний интеграл просто равен $$\vec{A}$$. Таким образом,

$$\vec{L}=\cfrac{Q}{4\pi c a}\int\!d(\cos\theta)\,d\varphi\,\vec{n}\times \left[\vec{\mathfrak{m}} \times \vec{n}\right].$$

Это выражение совпадает с (5).

Как и ожидалось, весь момент импульса, запасенный в постоянном электромагнитном поле, передается зарядам при исчезновении магнитного поля.