Простейшая модель электрона: электромагнитная масса и гиромагнитное отношение
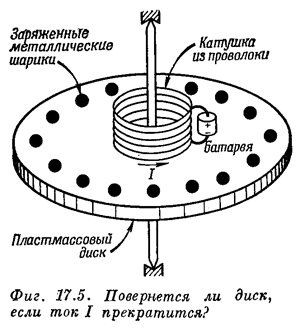
Продолжим развлекаться с классической электродинамикой. В прошлый раз мы подсчитали момент импульса в системе, состоящей из магнитного момента (маленькой катушки) в центре большой равномерно заряженной сферы
$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$(1)
Но магнитное поле вокруг сферы можно создать без дополнительной катушки, просто закрутив ее. Получается, что часть момента импульса вращающейся сферы запасается в ее электромагнитном поле. Определим эту добавку.
Магнитный момент вращающейся сферы
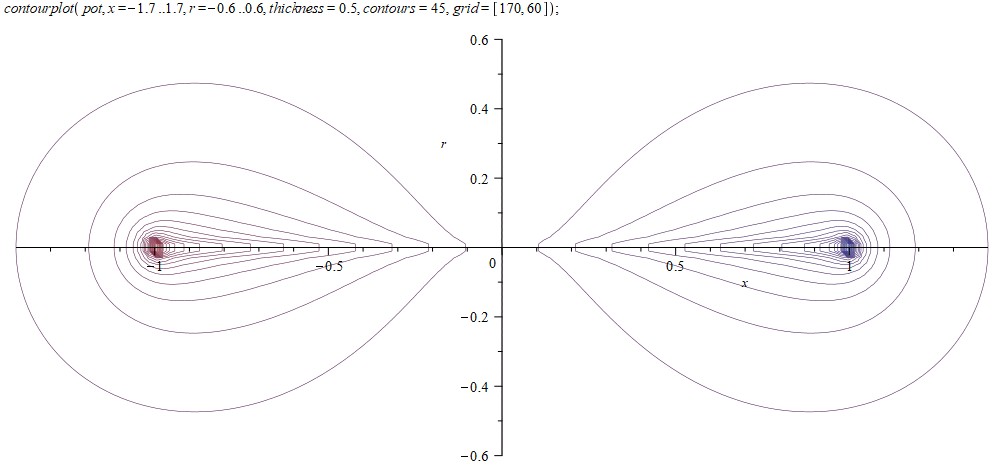
Мы собираемся показать, что магнитное поле вне равномерно заряженной сферы радиуса a и заряда Q, вращающейся с угловой скоростью ω, точно совпадает с полем магнитного диполя.
Начинаем с векторного потенциала
$$\vec{A}={1\over c}\int\!{\vec{j}\over r}\,dV={Q\over 4\pi ca^2}\int\!{\vec{v}\over r}\,dS={Q\over 4\pi ca^2}\int\!{\vec{\omega}\times a\vec{n}\over r}\,dS,$$
где $$r=|\vec{R}-a\vec{n}|$$ — расстояние от элемента поверхности dS, задаваемого
$$\vec{A}={Q\over 4\pi ca}\,\vec{\omega}\times\int\!{\vec{n}\over \sqrt{R^2 + a^2-2Ra\cos\chi}}\,dS={Q\over 4\pi ca}\,\vec{\omega}\times\vec{I}.$$
Интеграл $$\vec{I}$$ в последнем выражении — это усреднение единичного вектора $$\vec{n}$$ по направлениям с весом 1/r. Исходя из соображений симметрии ясно, что в результате интегрирования мы получим вектор, параллельный вектору $$\vec{R}$$. Подтвердим это вычислением.
В сферических координатах $$\inline \vec{n}=(\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta)$$. Направим вектор $$\vec{R}=(0,0,R)$$ вдоль оси z. Тогда угол χ между векторами $$\inline \vec{n}$$ и $$\inline \vec{R}$$ совпадает со сферической координатой θ. Z-компонента интеграла
$$I_z=a^2\int\!\cos\theta\,{1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}\,d(\cos\theta)\,d\varphi.$$
Известно, что функцию 1/r можно разложить по многочленам Лежандра (нас интересует область R > a)
$${1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}=\sum\limits_{l=0}^\infty{a^l\over R^{l+1}}P_l(\cos\theta).$$
Подынтегральное выражение состоит из произведения этого ряда на многочлен Лежандра $$P_1(\cos\theta)=\cos\theta$$. Тогда из условия ортогональности
$$\int\limits_{-1}^{1} P_k(x)P_l(x)\,dx={2\over 2k+1}\delta_{kl}$$
сразу следует ответ
$$I_z={4\pi\over 3}{a^3\over R^2}.$$
Компоненты Ix и Iy пропорциональны интегралам от периодических функций sin φ и cos φ, и поэтому равны нулю. Переходя от проекций к вектору, для векторного потенциала получаем
$$\vec{A}={Qa^2\over 3c}\,\vec{\omega}\times{\vec{R}\over R^3}.$$
Таким образом, магнитное поле вне вращающейся сферы совпадает с полем магнитного диполя
$$\vec{\mathfrak{m}}={Qa^2\vec{\omega}\over 3c}.$$(2)
Для полноты отметим, что аналогичными вычислениями легко показать однородность магнитного поля внутри вращающейся сферы.
Электромагнитная масса
Коэффициент в (1) можно переписать
Вслед за Фейнманом мы будем называть электромагнитной массой коэффициент пропорциональности между скоростью равномерного движения сферы и импульсом электромагнитного поля. В нерелятивистском случае
$$\vec{E}=Q{\vec{R}\over R^3},\quad\vec{H}={Q\over c}{\vec{v}\times\vec{R}\over R^3}.$$
Тогда импульс электромагнитного поля дается интегралом
$$\vec{P}={1\over 4\pi c}\int\!\vec{E}\times\vec{H}\,dV={Q^2\over 4\pi c^2}\int\!{1\over R^4}\,\vec{n}\times\left[\vec{v}\times\vec{n}\right]\,dV.$$
Такой интеграл (с точностью до коэффициента) мы вычисляли в прошлый раз, поэтому сейчас просто выпишем ответ
$$\vec{P}={2Q^2 \over 3 ac^2}\,\vec{v}=m_e \vec{v}.$$
Гиромагнитное отношение и модель электрона
Теперь мы можем переписать (1) в таком виде
$$\vec{L}={m_ec\over Q}\,\vec{\mathfrak{m}}.$$
Мы получили интересный результат: гиромагнитное отношение для вращающейся безмассовой заряженной сферы совпадает с гиромагнитным отношением электрона.
Обычно в литературе по квантовой механике утверждается, что нельзя представлять себе спин электрона как его вращение, так как в такой модели скорость точек на его поверхности будет больше скорости света. Сейчас мы в этом убедимся.
Подставим в (1) магнитный момент (2) и спин электрона ½:
$${\hbar\over 2}={2\over 3}\,{Q\over ca}\,{Qa^2\omega\over 3c},$$
откуда отношение экваториальной скорости к скорости света есть
$${a\omega\over c}={9\over 4}\,{\hbar c\over Q^2}={9\over 4\alpha}\approx308.$$
Несостоятельность простейшей модели электрона проявляется и в том, что полная энергия электрического поля
$$U={1\over 8\pi}\int\!{E^2}\,dV={1\over 8\pi}\int\limits_a^{\infty}{Q^2\over R^4}\,4\pi R^2\,dR={Q^2 \over 2a}={4\over 3}\,m_ec^2$$
отличается от ожидаемой величины mec2.
Комментарии
Я могу, кстати, написать еще один пост про задачу из «общей» физики, про брахистохрону под землей (в параболическом потенциале).
Забавно, что имено Паули, а не Гаудсмит и Уленбек получил Нобелевскую премию в соответсвующим вопросе (хотя Паули вне всякого сомнения ее заслужил).
Тогда только вышла статья Роя Керра о вращающейся черной дыре,
а в 1968 Картер выдвинул идею что это и есть электрон.
Эта статья и близкие идеи Уиллера поддержали идею, что электрон -- это
захваченный на кольцевую орбиту фотон, что затянуло меня очень надолго,
смотри мою статью в УФН 2024 (10), или короткую статью в PEPAN 2023.
Я уже очень стар (85), считать тяжело, но голова полна идей, и мне нужна
Ваша помощь в сотрудничестве, или как минимум, в построении графика (картинки).
Хотел написать Вам письмо, но не нашел Ваш email.
С уважением,
Александр
Оставьте свой комментарий