maple
Как создается электрическое поле в проводнике с током?
Мотивация
Вопрос, вынесенный в заголовок, в свое время породил большую дискуссию на физическом форуме (1, 2, 3). Вот более точная формулировка вопроса:
Рассмотрим длинный провод, подключенный к батарейке. По нему течет постоянный ток. Ток создается электрическим полем Е, которое, в свою очередь, создается зарядами на полюсах батарейки. Почему вдали от полюсов (например, в середине проводника) поле Е=const, а не убывает при удалении от полюсов, как ему положено по закону Кулона?
Правильный ответ заключается в том, что батарейка не является единственным источником электрического поля, какие бы процессы в ней ни происходили. На поверхности проводника с током возникают дополнительные заряды, которые и создают постоянное электрическое поле внутри.
Обоснование появления зарядов на поверхности проводника с током следующее. Плотность тока внутри проводника по закону Ома пропорциональна напряженности поля:
$$\vec{j}=\lambda \vec{E}.$$
Возьмем дивергенцию обеих частей и воспользуемся первым уравнением Максвелла $$\text{div}\vec{E}=4\pi\rho$$ и законом сохранения электрического заряда в локальной форме $$\text{div}\vec{j}=-\partial\rho/\partial t$$:
$$-{\partial\rho\over\partial t}=4\pi\lambda\rho.$$(1)
Так как протекание тока — стационарный процесс, в котором величины со временем не меняются, то производная в левой части зануляется, поэтому правая часть — плотность зарядов внутри проводника — тоже есть 0. Следовательно, поле в проводнике может создаваться только зарядами на его поверхности.
В этом посте попробуем найти, каким именно должно быть распределение поверхностного заряда, чтобы внутри проводника с постоянным сечением создалось однородное электрическое поле.
Близкая задача из электростатики
К сожалению, мы не можем найти точное распределение поверхностных зарядов по проводнику, если не учтем механизм того, как именно создается разность потенциалов на его концах. Вместо выбора такого механизма сделаем приближение, сказав что никакого механизма нет. Фактически, будем решать упрощенную задачу: как нужно распределить заряд по поверхности, чтобы поле внутри стало таким же, как и при стационарном протекании тока?
Разумеется, распределенный по поверхности проводника заряд без механизма создания разности потенциалов сразу же растечется (характерное время растекания можно найти из уравнения (1)), и, казалось бы, решать такую задачу бессмысленно. Но можно сформулировать задачу из электростатики о проводнике во внешнем однородном электрическом поле с точно таким же ответом:
Цилиндрический проводник длины l и радиуса R помещен во внешнее электрическое поле, так что его ось направлена по полю. Найти распределение поверхностных зарядов.
Действительно, в этом случае заряды так распределятся по поверхности проводника, что линейный потенциал внешнего поля $$\varphi_\text{внеш}=-|E|x$$ будет скомпенсирован их собственным потенциалом $$\varphi=kx$$ во всем объеме проводника.
Для полноты отметим, что аналогичная задача проводнике сферической формы имеет простое точное решение.
Наивный подход
$$ \newcommand{\drawCircle}[3]{ \draw (#1,#2) arc (90:270:#3 and #2); \draw[dashed] (#1,-#2) arc (-90:90:#3 and #2); } \newcommand{\drawTik}[2]{\draw (#1,0.1) -- ++ (0,-0.2) node[fill=white,below,inner sep=0,pos=1.4] {$#2$}} \begin{tikzpicture}[>=latex] \def\rx{4} \def\xx{-1.9} \def\x{1.9} \def\ry{1.2} \def\e{0.48} \node[above right,inner sep=2] at (0,\ry) {$R$} \node[below right,inner sep=2] at (0,-\ry) {$-R$} \node[below right] at (0,0) {$0$} \draw[->,very thin] (-\rx-1,0) -- (\rx+1,0) node[below] {$x$}; \draw[->,very thin] (0,-1.5*\ry) -- (0,2*\ry) node[left] {$r$}; \draw (\rx,0) ellipse (0.48 and \ry); \draw[] (-\rx,-\ry) -- (\rx,-\ry) (-\rx,\ry) -- (\rx,\ry); \drawCircle{-\rx}{\ry}{\e} \drawCircle{\xx-0.1}{\ry}{\e} \drawCircle{\xx+0.1}{\ry}{\e} \node[above] at (\xx,\ry) {$dx_1$} \drawTik{\xx}{x_1} \drawTik{\x}{x} \draw[dashed](\xx,\ry) -- (\x,0) \draw (\rx,0) ellipse (0.25 and 0.62); \draw (\rx,0) ellipse (0.3 and 0.75); \drawTik{-\rx}{-{l\over2}} \drawTik{\rx}{l\over2} \draw[dashed] (\x,0) -- (\rx,0.68) node[inner sep=2,pin={[pin distance=6, pin edge={<-,solid,black},fill=white,inner sep=1]30:$dr$}] {} \draw[->] (2.8,\ry+0.8) -- ++(2,0) node[pos=0.9,above] {$\vec{E}$}; \end{tikzpicture} $$
Обозначим плотность зарядов через $$\sigma_1(x)$$ на боковой поверхности и $$\sigma_2(r)$$ на поверхности оснований. Через эти величины можно выразить электрическое поле или потенциал внутри цилиндра, взяв интегралы по поверхности. Скажем, на оси цилиндра
$$\varphi(x)=\int\limits_{-l/2}^{l/2}{2\pi R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}+ \int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r) \over\sqrt{r^2+\left(x-{l\over2}\right)^2}} -\int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r)\over\sqrt{r^2+\left(x+{l\over2}\right)^2}} =Ex.$$(2)
Здесь учтены симметрии задачи: вращательная симметрия вокруг оси повлияла на выбор элементов площади, а зеркальная симметрия выражается в том, что плотности зарядов на основаниях цилиндра имеют противоположный знак ($$\sigma_2$$ и $$-\sigma_2$$), и в том, что функция $$\sigma_1(x)$$ — нечетная.
Мы получили интегральное уравнение на $$\sigma_1(x)$$ и $$\sigma_2(r)$$. Я не смог решить его в явном виде. Можно было бы рассмотреть предельный режим, когда $$l\gg R$$, и поискать приближенное решение в области $$|x|\ll l$$. Тогда вкладом двух последних интегралов можно пренебречь, а в первом интегрировать от минус бесконечности до бесконечности:
$$\int\limits_{-\infty}^{\infty}{R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}=x.$$(3)
Здесь я опустил коэффициент пропорциональности, не влияющий на дальнейшие рассуждения. Это интегральное уравнение имеет вид свертки ядра $$k(x)=1/\sqrt{1+x^2/R^2}$$ и искомой функции. Такое уравнение можно решить, взяв преобразование Фурье от обеих частей:
$${\cal F}(\sigma_1)\int {e^{-ikx}\over\sqrt{1+\dfrac{x^2}{R^2}}}dx=\int xe^{-ikx}dx.$$
Интегрирование по частям справа дает $$\inline\int xe^{-ikx}dx=-i\delta(k)/k$$. Искомая функция ищется через обратное преобразование Фурье:
$$\sigma_1(x)={-i\over2\pi}\int\dfrac{\delta(k)e^{ikx} dk}{k\int {e^{-iks}\over\sqrt{1+\frac{s^2}{R^2}}}ds}.$$
Пока оставим попытки решить интегральное уравнение и посмотрим, что нам предлагает математика, а именно раздел, изучающий уравнения математической физики.
Аналитические методы заводят в тупик
Наша задача на языке математики формулируется так. Вне цилиндра потенциал подчиняется уравнению Лапласа $$\Delta\varphi=0$$ и стремится к нулю (как поле диполя) на бесконечности. На поверхности цилиндра потенциал фиксирован и описывается начальными условиями
$$\begin{align*}\varphi(x, R)&=Ex,\quad x\in\left[-{l\over2},{l\over2}\right],\\ \varphi\left(\pm{l\over2}, r\right)&=\pm E{l\over2},\quad r\in\left[0,R].\end{align*}$$
Это формулировка задачи Дирихле для уравнения Лапласа. Решение у этой задачи существует и оно единственно. Потенциал определяет электрическое поле вне цилиндра, а скачок нормальной составляющей электрического поля на границе цилиндра пропорционален искомой поверхностной плотности заряда.
Уравнение Лапласа в цилиндрических координатах с учетом цилиндрической симметрии задачи записывается так:
$${1\over r}{\partial\over\partial r}\left(r{\partial\varphi\over\partial r}\right)+{\partial^2\varphi\over\partial x^2}=0.$$(4)
Стандартный метод решения таких уравнений — метод разделения переменных, он же метод Фурье. Искомая функция ищется в виде суммы (конечной, счетной или интеграла) произведений функций, в которых каждый сомножитель зависит только от своей переменной:
$$\varphi(x,r)=\Sigma_kX_k(x)R_k(r).$$
Мы хотим, чтобы (4) выполнялось не только для всей суммы целиком, но и для каждого элемента $$X_k(x)R_k(r)$$. Подставляем его в (4) и получаем:
$${1\over rR_k}{\partial\over\partial r}(rR_k')=-{1\over X_k}X_k''=-\lambda_k.$$
После такой подстановки получилось представить равенство так, что левая его часть зависит только от координаты r, а правая — только от координаты x. Равенство возможно, только если никакой зависимости нет, то есть и правая, и левая часть равны некоторой константе $$\lambda_k$$. Дальше, в зависимости от вида граничных условий, выбирается одно из двух получившихся дифференциальных уравнений
$$\left\{ \begin{array}{l} R_k'+rR_k''+\lambda_krR_k=0,\\ X_k''-\lambda_kX_k=0,\end{array} $$
и исследуется задача Штурма — Лиувилля: при каких $$\lambda_k$$ с учетом граничных условий у этого дифференциального уравнения возможны решения. Наконец, для этих $$\lambda_k$$ решается оставшееся дифференциальное уравнение и ответ обычно записывается в виде ряда по собственным функциям оператора Штурма — Лиувилля.
Проделать эту процедуру в нашем случае не представляется возможным. Дело в том, что первое уравнение нужно решать на области $$r\in[R,\infty)$$, когда $$x\in\left[-{l/2},{l/2}\right]$$, и на области $$r\in[0,\infty)$$ в противоположном случае. Аналогично со вторым уравнением. Представить решение по всему пространству вне цилиндра в виде одного ряда по собственным функциям
Численное решение
Возвращаемся к интегральному уравнению (2) из наивного подхода. Зададимся
$$\int\limits_{-1}^{1}{dx_1\,\sigma_1(x_1)\over\sqrt{1+10000(x-x_1)^2}}+ \int\limits_{0}^{0,01}r\,dr\,\sigma_2(r)\left({1 \over\sqrt{r^2+\left(x-1\right)^2}} -{1\over\sqrt{r^2+\left(x+1\right)^2}}\right) =x.$$
Приближение к его решению можно искать не на всех функциях, а на определенном классе функций, например, на нескольких первых слагаемых разложения в степенной ряд. Отклонение получающейся функции $$\widetilde{\varphi}_a(x)$$ от правой части будем оценивать как интеграл от квадрата разности, и будем подбирать параметры функций a, добиваясь минимума этого интеграла:
$$f(a)=\int\limits_{-1}^{1}\left(\widetilde{\varphi}_a(x)-x\right)^2dx\to \text{min}.$$
Как обычно, решение попробовал найти в Maple. У меня не получилось заставить его минимизировать такой интеграл, зависящий от набора параметров. Поэтому я оставлял только один параметр, заменяя остальные их текущими значениями, строил график по этому параметру и определял его текущее значение в минимуме. Фактически выполнял вручную итерации из метода координатного спуска для функции $$f(a)$$ такого типа:
f := a -> int((
int((11.485*s + 0.584*s^3 + 0.883*s^5 + 0.587*s^7 + 0.2*s^9 + 3.57*s^11)/
sqrt(1 + 10000*(x - s)^2), s = -1 .. 1, numeric) +
int((5.01 + 5.46*10^2*r + 5.71*10^5*r^2 + 3.62*10^6*r^3 + 42.35*10^8*r^4 + a*r^5)*
r*(1/sqrt(r^2 + (1 - x)^2) - 1/sqrt(r^2 + (x + 1)^2)), r = 0 .. 0.01, numeric)
- x)^2, x = -1 .. 1, numeric)Здесь все интегралы отмечены как «numeric», чтобы Maple не пытался вычислить их аналитически. В моем случае попытка аналитического вычисления существенно замедляла работу, так что я не мог дождаться результата. Потенциал на оси для моего приближения на глаз отличается от прямой только у краев:
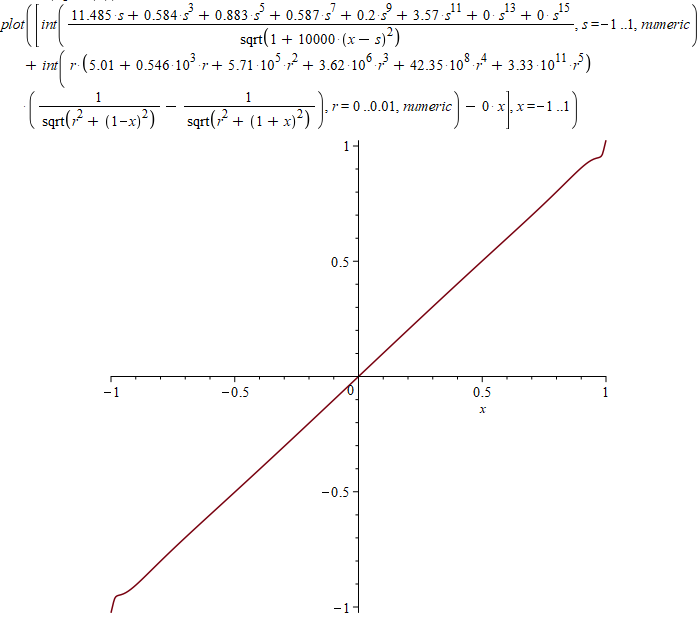
График отклонения от прямой (интеграл от квадрата этой функции я минимизировал, здесь масштаб по осям разный):
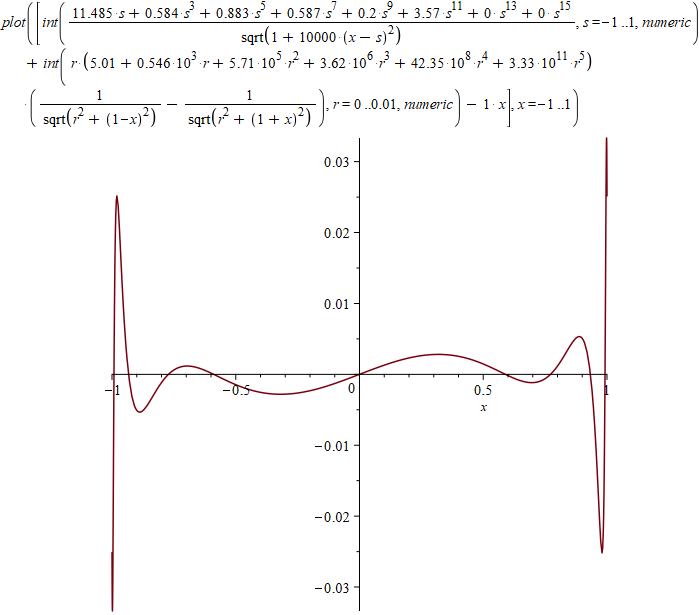
Можно также нарисовать графики плотностей на основаниях и на боковой поверхности:
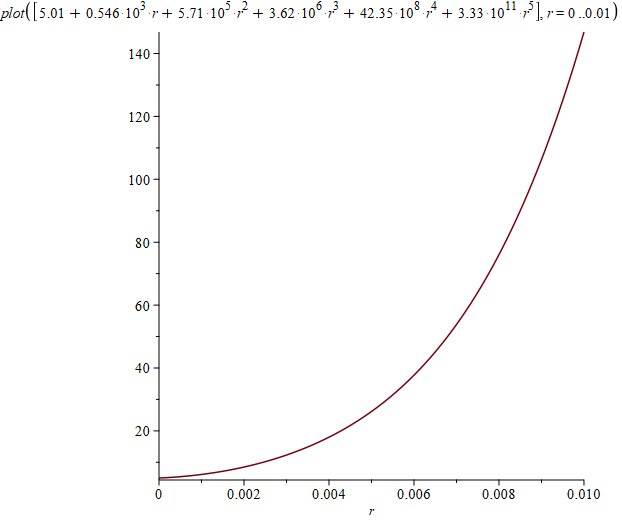
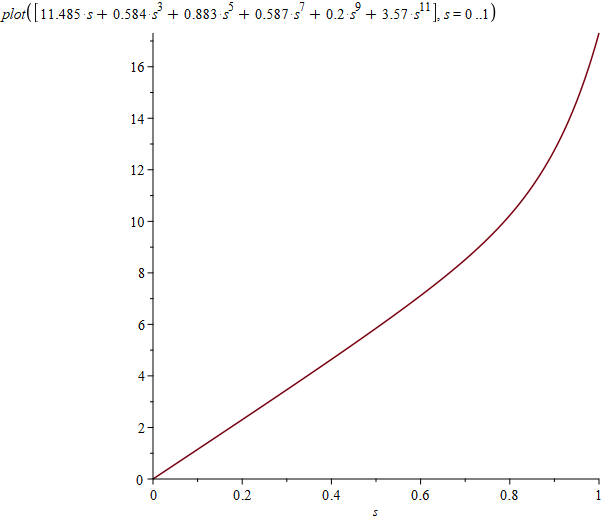
Перейдем теперь к исследованию этого решения по всему пространству. Чтобы найти потенциал в произвольной точке не на оси, нужно добавить интегрирование по углу, так как теперь расстояние от элемента поверхности до расчетной точки уже зависит от угла. Трехмерный график потенциала выглядит так:
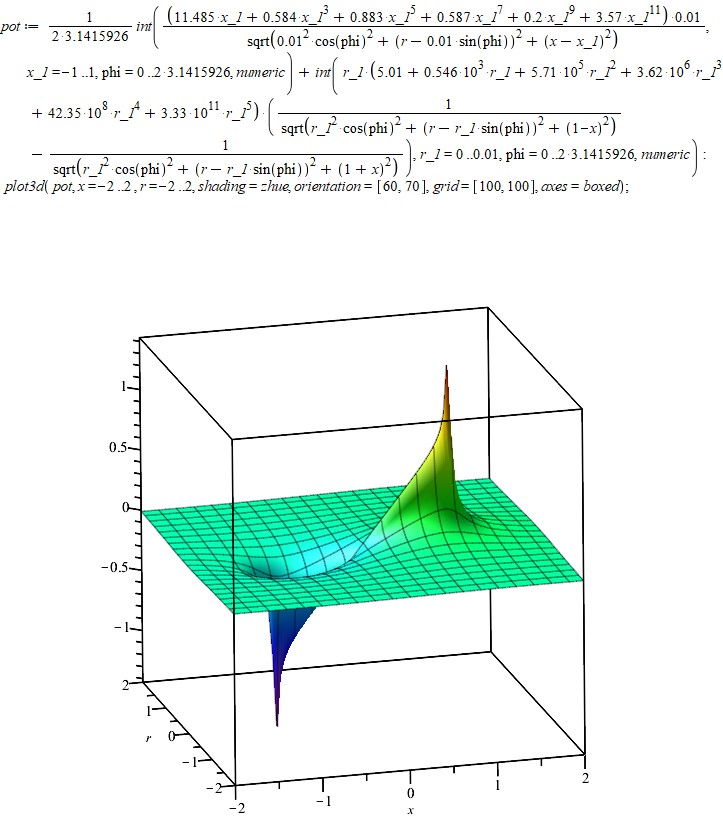
Нарисуем сечения эквипотенциальных поверхностей:
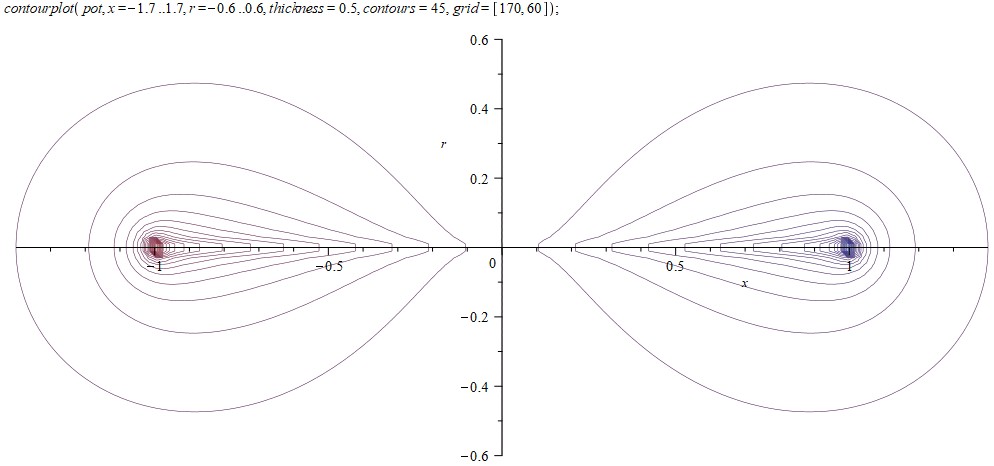
Рассмотрим поближе край проводника:
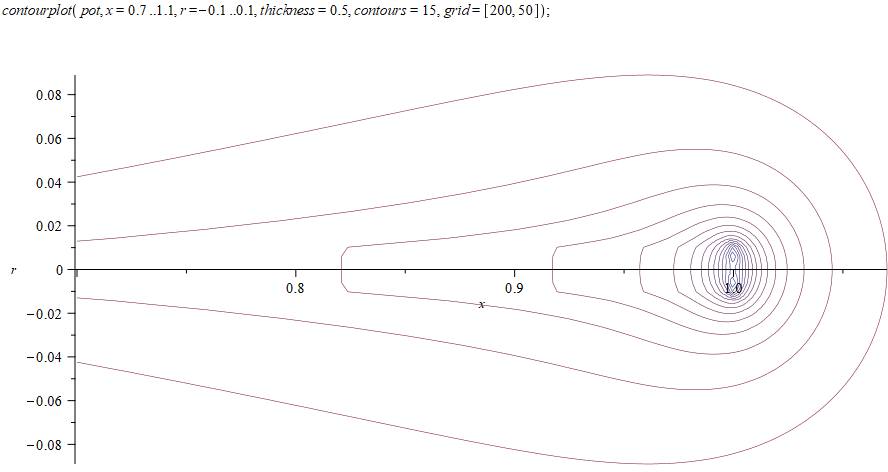
На полученный потенциал можно наложить внешнее электрическое поле и проверить, какая будет поверхность нулевого потенциала. Для правильного решения она должна совпадать с цилиндрической поверхностью проводника. В нашем случае у его краев (от 0,7 до 1) наблюдаются заметные утолщения, наглядно показывающие степень полученного приближения:
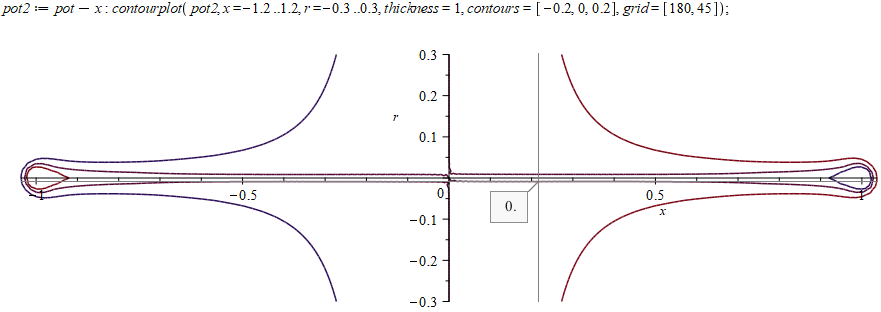
Вывод
Мы пытались решить две близких задачи: одна об электрическом поле внутри и снаружи провода с током, вторая о разделении зарядов в проводнике во внешнем электрическом поле. Аналитические методы не привели к успеху. Пришлось искать приближенное численное решение в Maple и использовать встроенные инструменты визуализации решения.
Из этого
Брахистохрона под землей
Мотивация
В сборниках задач по физике часто встречается известная задача о свободном падении тела сквозь прямой тоннель, проходящий через центр Земли и соединяющий диаметрально противоположные точки. Для решения нужно знать, что сила притяжения к центру Земли в таком тоннеле уменьшается линейно до нуля, и тело, упавшее в такой тоннель, будет совершать гармонические колебания. Время движения составляет половину периода и для модели однородной Земли составляет 42 минуты. Более того, это время не меняется для любого прямого тоннеля, идущего по хорде (не проходящего через центр), если трением можно пренебречь.
Также в популярных книгах и других источниках есть задача о брахистохроне — кривой скорейшего спуска. В ней требуется найти форму желоба, проложенного между двумя фиксированными точками A и B, чтобы время скатывания тела из A в B было наименьшим. В однородном гравитационном поле брахистохроной является дуга циклоиды.
Вполне естественным кажется желание скрестить эти две задачи и выяснить, какой формы нужно проложить тоннель под землей, чтобы в идеальной ситуации без трения между точками A и B на поверхности (скажем, между двумя городами) поезд проезжал за наименьшее время. Эта новая задача имеет аналитическое решение. Её ответом является гипоциклоида — кривая, которую описывают точки окружности радиуса $$a$$, катящейся без проскальзывания внутри другой окружности радиуса $$b$$. Вот как записывается параметрическое уравнение гипоциклоиды и выглядит ее чертеж:
$$\left\{\begin{array}{lr} x=(b-a)\cos \theta+a\cos(b-a)\theta,\\ y=(b-a)\sin\theta-a\sin(b-a)\theta. \end{array}\right.$$
$$\begin{tikzpicture} \def\clr{black} \def\a{1} \def\b{5} \newcommand{\xt}[1]{(\b-\a)*cos(#1)+\a*cos((\b-\a)*#1/\a} \newcommand{\yt}[1]{(\b-\a)*sin(#1)-\a*sin((\b-\a)*#1/\a} \draw[cyan,very thin] (-\b-1,-\b-1) grid (\b+1,\b+1); \draw[->] (-\b-1,0) -- (\b+1,0); \draw[->] (0,-\b-1) -- (0,\b+1); \draw[\clr,thick] (0,0) circle (\b); \draw[\clr,dashed,very thin] (0,0) circle (\b-\a); \draw[line width=2pt,orange!80!red] plot[samples=60,domain=0:\a*360,smooth,variable=\t] ({\xt{\t}},{\yt{\t}}); \def\t0{40} \draw[\clr!50!black] (\t0:\b-\a) circle (\a); \draw[purple,fill] ({\xt{\t0}},{\yt{\t0}}) circle (2pt) -- (\t0:\b-\a) circle (1pt) node [midway, sloped, above] {\scriptsize $a$} -- (0,0) circle (1pt) node [midway, sloped, above] {\scriptsize $b-a$} node [below right] {$O$}; \node[\clr,fill=white,text width=1cm,align=center] at (-\b,\b) {$a=\a$ $b=\b$}; \end{tikzpicture}$$
Я задумался об этой задаче в старших классах или на первом курсе института, но тогда, разумеется, у меня не хватало знаний для решения в аналитическом виде. Я вернулся к задаче на четвертом курсе и смог довести вычисления до конца, не обращаясь к источникам, но и не без помощи Maple. Эти вычисления были одними из самых сложных среди всех задач с явным аналитическим ответом, которые я решал.
Физическая сторона задачи
$$\begin{tikzpicture} \def\a{1} \def\b{5} \draw ([shift=(-10:\b)]0) arc (-10:90:\b); \draw[-stealth] (\b,0) node[right]{$A$} -- node[pos=0.92,above,inner sep=2] {$\varphi$} (0,0) -- (\b*0.35,\b*0.6) node[below,pos=0.9]{$\vec{r}$} ; \node[above] at (\b*0.32,\b*0.95) {$B$}; \draw[line width=1pt,orange!80!red] plot[samples=12,domain=0:72,smooth,variable=\t] ({(\b-\a)*cos(\t)+\a*cos((\b-\a)*\t/\a},{(\b-\a)*sin(\t)-\a*sin((\b-\a)*\t/\a}); \end{tikzpicture}$$
Движение поезда по подземному тоннелю будем рассматривать в полярных координатах. Считаем потенциал внутри Земли осцилляторным: $$U\sim r^2$$. Запишем закон сохранения энергии с учетом нулевой скорости поезда на поверхности:
$${mv^2\over 2}+{m\omega^2r^2\over 2}={m\omega^2r_0^2\over 2},$$(1)
где $$r_0$$ — радиус Земли, $$\omega=2\pi/T$$ — круговая частота колебаний, соответствующая периоду в 84 минуты. Время движения через тоннель $$\inline t=\int{dl\over v}$$. Выражаем скорость $$\inline v=\omega\sqrt{r_0^2-r^2}$$ из (1) и для времени движения поезда через тоннель получаем следующее выражение:
$$t=\int{dl\over v}={1\over\omega}\int{\sqrt{dr^2+r^2d\varphi^2}\over\sqrt{r_0^2-r^2}}={1\over\omega}\int{\sqrt{r'^2+r^2}\over\sqrt{r_0^2-r^2}}d\varphi,$$
Здесь мы выразили элемент длины пути через полярные координаты. Таким образом, задача свелась к поиску функции $$r(\varphi)$$ с фиксированным значением $$r(\varphi_A)=r(\varphi_B)=r_0$$ на концах отрезка, для которой функционал
$$\omega t=\int\limits_{\varphi_A}^{\varphi_B}\sqrt{{r'^2+r^2}\over{r_0^2-r^2}}d\varphi$$(2)
принимает наименьшее значение.
Математическая сторона задачи
Задача по минимизации интеграла (2) на множестве достаточно хороших с точки зрения физика функций (скажем, дифференцируемых сколько нужно раз) — типовая задача вариационного исчисления. Заметим, что подынтегральное выражение в (2) можно представить в виде функциональной зависимости от $$r$$ и ее производной:
$${\cal L}(r,r')=\sqrt{{r' ^2+r^2}\over{r_0^2-r^2}}$$(3)
Из курса дифференциальных уравнений известно, что экстремальные значения (2) нужно искать на решениях дифференциального уравнения Эйлера — Лагранжа:
$${\partial{\cal L}\over\partial r}-{d\over d\varphi}{\partial{\cal L}\over\partial r'}=0.$$
Если вы вооружитесь бумагой и ручкой и попробуете подставить сюда (3), то быстро заметите сложность получившегося дифференциального уравнения со второй производной и нагромождением корней и осознаете тупиковость этого подхода. В системах компьютерной алгебры есть встроенные пакеты для решения вариационных задач. Вот пример для Maple, где вы видите трехэтажное дифференциальное уравнение:
Кроме того, Maple заботливо подсказывает, что у получившегося дифференциального уравнения есть первый интеграл.
И тут вы вспоминаете, что на курсах теоретической механики и дифференциальных уравнений
$${\cal L}-r'{\partial{\cal L}\over\partial r'}=const.$$
Если вам проще воспринимать физику, а не математику, вы можете представить некоторую систему, описываемую функцией Лагранжа (3). Движение во «времени» $$\varphi$$ от «момента» $$\varphi_A$$ к $$\varphi_B$$ будет происходить по такой траектории $$r(\varphi)$$, на которой «действие» (2) примет экстремальное значение. Так как функция Лагранжа $$\cal L$$ не зависит от «времени» $$\varphi$$, то у системы есть сохраняющаяся величина — «энергия». Первый интеграл выше как раз и дает величину этой «энергии».
Выполним дифференцирование:
$$k={\cal L}-r'{\partial{\cal L}\over\partial r'}=\sqrt{{r' ^2+r^2}\over{r_0^2-r^2}} -r'{r'\over\sqrt{r_0^2-r^2}\sqrt{r'^2+r^2}}={r^2\over\sqrt{r_0^2-r^2}\sqrt{r'^2+r^2}}.$$
Мы пришли к дифференциальному уравнению первого порядка $$\inline r^2=k\sqrt{r'^2+r^2}\sqrt{r_0^2-r^2}$$, в котором разделяются переменные и получается следующий интеграл:
$$\varphi=\int{dr\over\sqrt{\cfrac{r^4}{k^2(r_0^2-r^2)}-r^2}}.$$
Его можно вычислить аналитически. Например, Maple выдает такой результат:
Чтобы доказать, что это выражение описывает гипоциклоиду, нужно взять её параметрическое уравнение и проделать достаточно громоздкие преобразования обратных тригонометрических функций, которые я не буду сейчас приводить.
В интернете опять кто-то неправ, или учимся избегать ошибок
Когда я занимался этой задачей, мне попадалась статья с нестандартными вычислениями: вместо полярных координат использовались декартовы. Тогда мне показалось, что автору очень повезло: уравнение гипоциклоиды в параметрической форме написано в таком виде, что параметр оказался пропорциональным физическому времени. При подготовке этой заметки я опять наткнулся на ту же статью. Сейчас эти нестандартные вычисления кажутся мне ошибочными.
Я предположил, что это
Вот ключевой момент статьи, в котором делается попытка доказать, что гипоциклоида — искомое решение:
Вопросы начинаются с формулы (19), в которой пропущен дифференциал, и поэтому не совсем понятно, по какому параметру дальше берутся производные. Эти же производные сохраняются вплоть до (22), куда подставляются $$x(t)$$ и $$y(t)$$ из (24) и (25). Но параметр $$t$$ в (24) и (25) не может быть временем $$t_\text{физ}$$, так как он является аргументом тригонометрических функций и должен быть безразмерным. Получается, это некоторый параметр, задающий положение точки на траектории, но не являющийся временем.
(Попутно возникает
Еще возникает вопрос о степенях свободы. В уравнениях (19) и (22) неизвестные величины — $$(x, y, t)$$. Таким образом, эти уравнения содержат лишнюю степень свободы по сравнению с неизвестными $$(r, \varphi)$$ из нашего рассмотрения (и из предыдущего раздела работы Аманды). Эта избыточность мешает корректному применению формализма Лагранжа — Эйлера. Какие признаки этого мы видим?
-
(22) — не единственное возможное следствие из (20) и (21). Если поделить (20) на (21), получим, что $$(y'/x')^2=(dy/dx)^2=const$$, а это есть уравнение, описывающее не гипоциклоиду, а прямую траекторию. Почему это следствие из (20) и (21) менее правильное, чем (22)?
-
(22) с точностью до константы $$C$$ по форме совпадает с законом сохранения энергии, с которого начиналось решение. Действительно, выражение в левой части напоминает квадрат скорости, а в правой — разницу квадратичных потенциалов, то есть изменение потенциальной энергии. Присутствие константы $$C$$ объясняется тем, что производные в (22) берутся не по физическому времени $$t_\text{физ}$$, а по другому параметру $$t$$, который в $$C$$ раз меньше: $$t_\text{физ}=Ct$$. Если бы связь $$t_\text{физ}=Ct$$ нарушилась, то (22) противоречило бы закону сохранения энергии. Таким образом, (22) можно получить без применения лагранжева формализма, просто напрямую из закона сохранения энергии с помощью замены $$t_\text{физ}=Ct$$. Следовательно, (22) не может иметь большего физического содержания, чем закон сохранения энергии, и не несет информацию о траектории, минимизирующей время.
-
(24) и (25) формально являются решением (22), так как зануляют его при выполнении (26). Но они не являются единственным решением. Фактически, любое физически возможное движение
из-за сохранения энергии будет удовлетворять уравнению (22). Важно лишь выбрать параметризацию этого движения так, чтобы физическое время было пропорционально параметру. Возьмем для примера движение по хорде $$x(t)=A$$, $$y(t)=B\cos t$$, где $$\inline A^2+B^2=R^2$$, подставим в (22) и при должном выборе константы $$C$$ (то есть при выборе правильного движения во времени вдоль хорды) получим тождество:
$$RB^2\sin^2 t=gC^2(R^2-A^2-B^2\cos^2 t)=gC^2B^2\sin^2 t.$$
Таким образом, осцилляторное движение по тоннелю в виде прямой хорды также является решением (22). Но оно отнюдь не минимизирует функционал (19) для общего времени движения между двумя точками.
Я так и не смог понять, можно ли провести рассуждения в декартовых координатах с избыточной степенью свободы и получить правильный ответ. Понятно желание использовать декартовы координаты, а не полярные, так как в них уравнение гипоциклоиды выглядит проще. Но интуитивно кажется, что лишняя степень свободы, появившаяся в функционале времени и соответствующая выбору закона движения тела вдоль траектории, не дает при применении лагранжева формализма достаточных ограничений на траекторию.
Я оставил комментарий в блоге Аманды с вопросами. Но никакой реакции не последовало.
Напишите свой комментарий, если видите ошибку в моих рассуждениях, или если знаете, как сделать корректное рассмотрение в декартовых координатах.
Добавлено 13.10.2023: я нашел у себя в архиве файлов сохраненную в 2008 году статью о брахистохроне, и это не работа Аманды. Автор не указан, статья располагалась по этой ссылке. Ход решения в этих статьях одинаков, но видно, что написаны они
Хоккейная задача — 2
Продолжим решать «хоккейную задачу». В прошлом посте мы рассмотрели вариант задачи с искусственной поддержкой постоянной скорости вращения кольца. Перейдем теперь к варианту, когда за счет трения замедляется не только поступательное движение, но и вращение.
Напомним, что динамика кольца описывается уравнениями
$$\begin{align*} {du\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{u-v\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}},\\ {dv\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{v-u\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}}, \end{align*}$$(1)
где $$v$$ — скорость поступательного движения, $$u=\omega R$$ — скорость вращательного движения кольца.
Система уравнений (1) симметрична относительно замены $$u$$ на $$v$$. Если в начальный момент $$u=v$$, то по соображениям симметрии это соотношение будет сохраняться между скоростями вплоть до остановки. Другой случай, который мы рассмотрим — это $$u>v$$. Противоположный случай $$u<v$$ будет вытекать из него простой заменой $$u$$ на $$v$$ из тех же соображений симметрии.
Вырожденный случай u = v
Оба уравнения системы принимают один и тот же вид
$${dv\over dt}=-\int\limits_0^{2\pi}{d\alpha\over 2\pi\sqrt2}\,\sqrt{1-\sin\alpha}={2\over\pi}.$$
Скорости совместного движения падают линейно со временем, но в $$\pi/2=1,\!57$$ раз медленнее отдельного вращения или отдельного поступательного движения.
Случай u > v
К сожалению, интегралы в системе (1) сводятся к эллиптическим, что не оставляет надежды решить систему аналитически. Остается численное решение.
Прямая попытка решить уравнение в Maple проваливается. Определенные интегралы заменяются нагромождением эллиптических интегралов, приводить которое здесь нет смысла. При построении графика мы видим сообщение об ошибке
Warning, cannot evaluate the solution past the initial point, problem may be complex, initially singular or improperly set up
Чтобы упростить выражения, накладываем ограничение $$u(t)\ge v(t)\ge 0$$ на каждый из интегралов.
sys_ode := {
diff(u(t), t) = -`assuming`(
[int(
(u(t)-v(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
)/(2*Pi),
diff(v(t), t) = -`assuming`(
[int(
(v(t)-u(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
)/(2*Pi), u(0) = 10, v(0) = 1
};Ограничения устраняют сообщение об ошибке. Maple надолго задумывается, но выводит пустой график. Чтобы понять причину, выведем решение уравнения в
p := dsolve(sys_ode, type = numeric):
p(1);$$[t=1.,\\u(t)=10.9976102709142-2.84005015829721 10^{-8}{\rm I},\\v(t)=1.04887416587408+2.92542849266058 10^{-8}{\rm I}]$$
Накопление ошибки округления приводит к появлению ненулевой мнимой части в искомых функциях,
sys_ode := {
diff(u(t), t) = -Re(`assuming`(
[int(
(u(t)-v(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
))/(2*Pi),
diff(v(t), t) = -Re(`assuming`(
[Re(int(
(v(t)-u(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
alpha = 0 .. 2*Pi
)],
[u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
))/(2*Pi), u(0) = 10, v(0) = 1
};Наконец, Maple, долго думая, всё же рисует график.
plots[odeplot](p, [
[t, (10-t), color=gray],
[t, sqrt(1-(1/10)*t), color=gray],
[t, u(t), color = blue],
[t, v(t), color = red]
], 0 .. 11);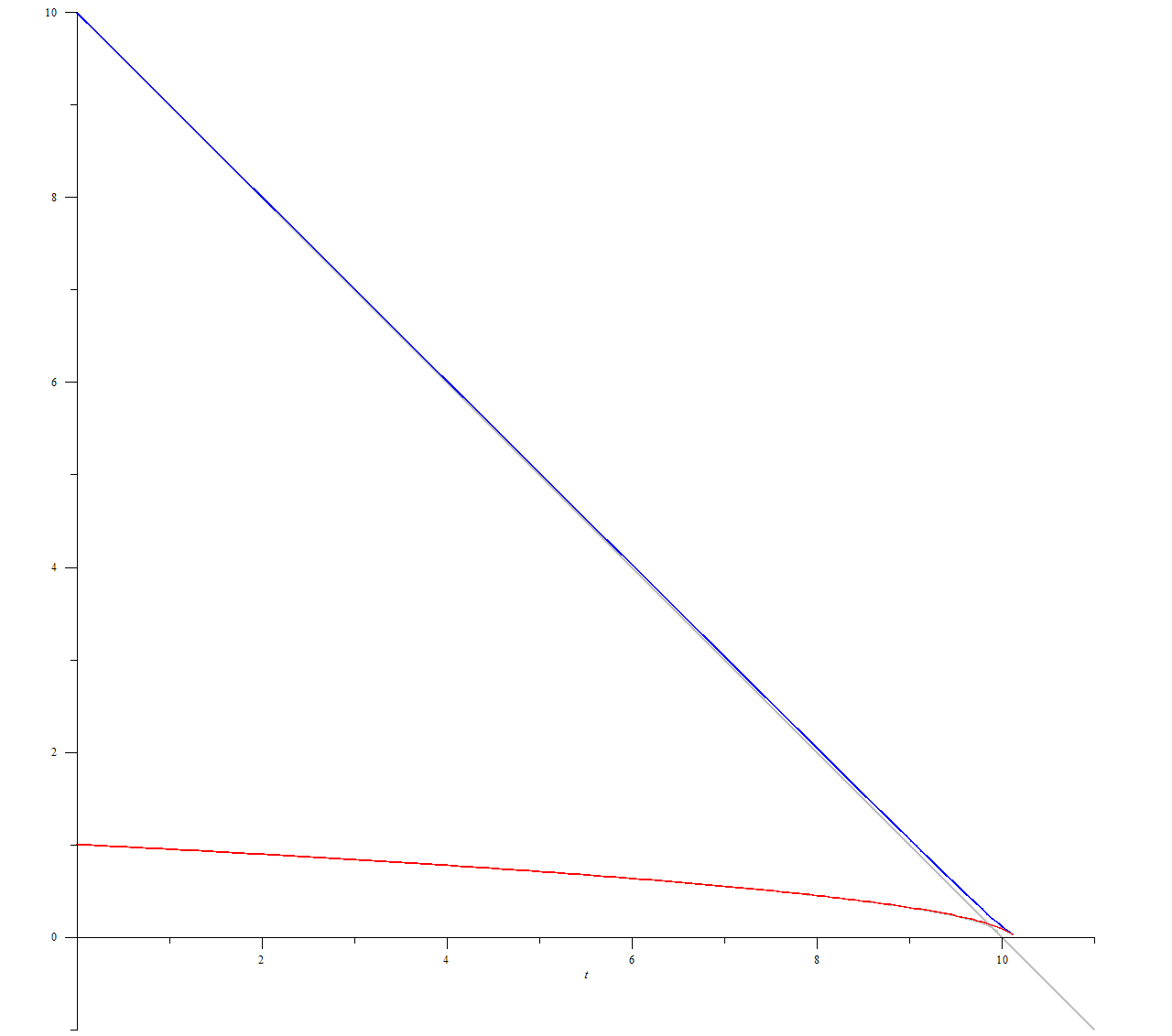
При этом мы видим предупреждение о точке остановки вычислений, которая, очевидно, совпадает с моментом окончания движения:
Warning, cannot evaluate the solution further right of 10.155665, probably a singularity
Для численного решения мы выбрали начальную поступательную скорость 1 и скорость вращения 10. Без вращения кольцо перемещается в течение 1 единицы времени на расстояние 0,5. Наличие вращения привело к тому, что поступательное движение сохранялось более 10 единиц времени.
Линеаризованное решение при u >> v
График $$u(t)$$ — синяя линия — практически совпадает с прямой. График $$v(t)$$ — красная линия — напоминает параболу. Такое поведение предсказывается линеаризованным решением в пределе $$u\gg v$$. Пренебрегая $$v$$ в первом уравнении системы (1) и раскладывая второе по степеням $$p=v/u$$, получаем
$$\begin{align*} {du\over dt}&=-1,\\ {dv\over dt}&=-{v\over 2u}. \end{align*}$$(2)
Решением этой системы являются функции $$u(t)=u_0-t$$, $$v(t)=v_0\sqrt{1-t/u_0}$$. Их графики изображены серыми линиями.
Как видим из численного решения и графика, приближение верно описывает характер движения, пока $$u$$ и $$v$$ не становятся сравнимыми. Вот график для случая, когда одна скорость в два раза больше другой:
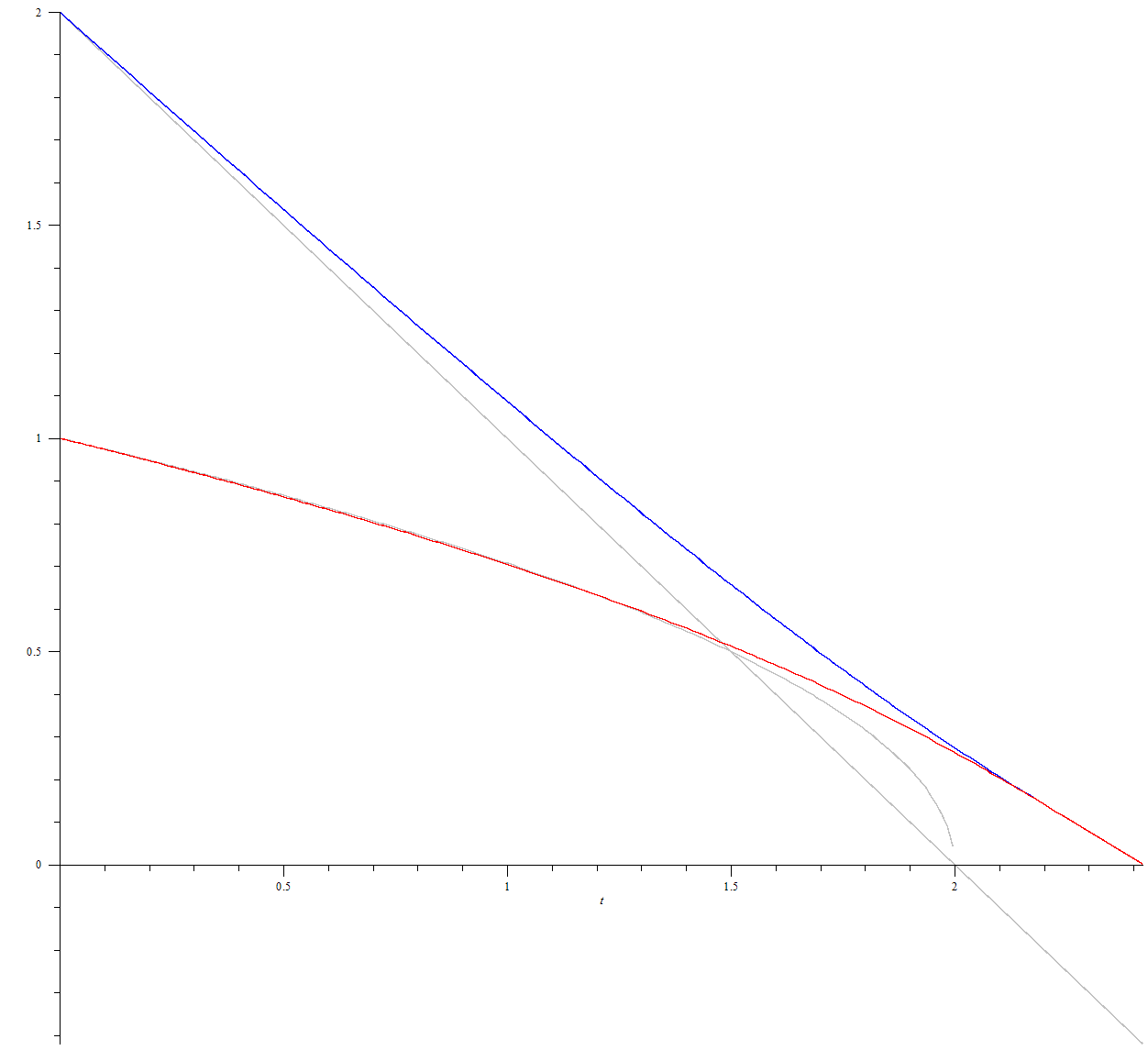
Здесь отличие от линеаризованного решения заметно практически сразу.
Путь до остановки: линеаризованное приближение
Пройденный кольцом путь дается площадью криволинейной трапеции под красной линией. В линеаризованном приближении криволинейная трапеция ограничена параболой и, как легко видеть, имеет площадь $$l=2u_0v_0/3$$. Если бы кольцо не вращалось, оно прошло бы расстояние $$l_0=v_0^2/2$$. Таким образом, чтобы увеличить проходимый путь в 5 раз, нужно закрутить кольцо с угловой скоростью
$$\omega_0={u_0\over R}={15\over 4}{v_0\over R}.$$
Напомним, что для прохождения кольцом того же пути при постоянном поддержании вращения его скорость должна быть в три раза меньше: $$\omega_0=(5/4)\,{v_0/R}$$.
Путь до остановки: численное решение
Теперь вычислим проходимый путь из первоначальных уравнений, без линеаризации.
Maple
dsol2p := dsolve(sys_ode, type = numeric, output = listprocedure):
v := eval(v(t), dsol2p):
v(4.04);$$0.00664275658541608$$
v(4.05);$$0.000276558860981139$$
v(4.06);$$0.00946581059191108$$
int(v(t), t = 0 .. 4.05);$$2.5535588257745343$$
Последний результат Maple вычислял больше 10 минут. Как видим, для начального значения 15/4 погрешность линеаризованного приближения составляет 2%.
Вывод
Мы решили «хоккейную задачу» в исходной упрощенной формулировке и без упрощений в линеаризованном приближении. С помощью системы компьютерной алгебры Maple убедились, что для условия этой задачи линеаризованное приближение дает ошибку на несколько процентов.
Хоккейная задача
В 2007 году на физтеховской олимпиаде по физике была такая задача:
Тонкое кольцо лежит на шероховатой горизонтальной поверхности. После толчка в направлении центра кольца оно перемещается на некоторое расстояние. Когда это кольцо раскрутили до некоторой угловой скорости (поддерживаемой постоянной за всё время движения), то при той же начальной скорости кольцо прошло в $$k$$ раз большее расстояние. Как было раскручено это кольцо? (попытайтесь в ответе найти нелинейную поправку). (В.С. Булыгин)
На примере этой задачи я хочу показать, как использовать системы компьютерной алгебры, в частности, Maple.
В условии поддержка постоянной угловой скорости вращения выглядит искусственно. Это требование упрощает задачу, чтобы ее можно было решить на олимпиаде. В этом посте рассмотрим такую формулировку, а в следующем — потерю через трение не только поступательной скорости, но и вращательной.
Физическая сторона задачи
Решение задачи разобрано на Элементах (там ее назвали «хоккейной задачей»). Физическая часть решения не требует выхода за рамки школьных знаний, на ней останавливаться не будем. А вот на математике остановимся подробнее. Начнем с системы уравнений, выведенной по ссылке выше:
$$\begin{align*} {du\over dt}&=-\mu g\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{u-v\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}},\\ {dv\over dt}&=-\mu g\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{v-u\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}}. \end{align*}$$(1)
Здесь $$v$$ — скорость поступательного движения, $$u=\omega R$$ — скорость вращательного движения кольца.
Уравнения таковы, что соответствующим выбором единицы измерения времени мы можем избавиться от несущественного множителя $$\mu g$$, поэтому в рассуждениях ниже мы его опустим.
Предельный режим
В предположении $$u=const$$ уравнение на $$v$$ имеет простой предельный режим, когда $$v\to 0$$. Тогда раскладывая подынтегральное выражение в ряд по $$v$$ с точностью до второго порядка малости и интегрируя, видим, что убывание скорости пропорционально самой скорости. При малых скоростях кольцо останавливается по экспоненте, как будто трение не сухое, а жидкостное.
Случай постоянной скорости вращения
По условию угловая скорость вращения поддерживается постоянной, а линейная скорость падает до 0. Логично предположить, что мы имеем дело с режимом $$0<v<u=\text{const}$$. Пусть $$p=v/u$$. Тогда
$$u{dp\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{p-\sin\alpha\over\sqrt{1+p^2-2p\sin\alpha}}.$$(2)
До остановки кольцо проходит расстояние
$$l=\int\limits_0^{t_\text{ост}} v\,dt=u\int\limits_0^{t_\text{ост}} p\,dt.$$(3)
Подставим $$dt$$ из (2) в (3):
$$u^2\int\limits_{p_0}^0{p\,dp\over-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{p-\sin\alpha\over\sqrt{1+p^2-2p\sin\alpha}}}=u\int\limits_0^{t_\text{ост}} p\,dt=l.$$(4)
Когда вращения нет, кольцо движется равнозамедленно и проходит расстояние $$l_0=v_0^2/2$$. Вращающееся кольцо проходит в $$k=5$$ раз большее расстояние $$l$$:
$$l=kl_0=k\,{v_0^2\over 2}=ku^2\,{p_0^2\over 2}.$$
Подставим $$l$$ в (4) и поделим на $$p_0^2$$:
$${1\over p_0^2}\int\limits^{p_0}_0{p\,dp\over\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{p-\sin\alpha\over\sqrt{1+p^2-2p\sin\alpha}}}={k\over 2}.$$(5)
Это уравнение дает нам соотношение между начальной скоростью вращения кольца $$\omega_0=v_0/(p_0R)$$ и ростом проходимого до остановки расстояния $$k$$.
Численное решение в Maple
Внутренний интеграл выражается через эллиптические интегралы. Однако Maple ничего не знает про знак $$p$$ и выдает слишком громоздкое выражение, содержащее фрагменты вроде $$\sqrt{-{2p/(p-1)^2}}$$, csgn(p-1). Подскажем очевидное ограничение на $$p$$:
`assuming`([
int(
(p-sin(alpha))/(2*Pi*sqrt(p^2 + 1 - 2*p*sin(alpha))),
alpha = 0 .. 2*Pi
)
], [p > 0]):
factor(%);
$${\left(p-1\right)\mathrm{EllipticK}\left(\dfrac{2\sqrt{p}}{p+1}\right)+\left(p+1\right)\mathrm{EllipticE}\left(\dfrac{2\sqrt{p}}{p+1}\right)\over p\pi}$$
После этого легко подобрать ответ $$p_0$$ с нужной точностью:
p0 := 0.78:
(int(
p^2 * Pi / (
(p-1) * EllipticK(2*sqrt(p)/(p+1)) +
(p+1) * EllipticE(2*sqrt(p)/(p+1))
),
p = 0 .. p0
)) / p0^2;
$$2.491446599$$
В начальный момент скорости поступательного движения и вращения были связаны соотношением $$v_0\approx0,\!78\,\omega_0R$$.
Приближенный ответ можно получить не только численно, но и из разложения внутреннего интеграла в ряд
expand(series(`assuming`([int(...)], [p >= 0]), p = 0, 8));
$${1\over 2}p+{1\over 16}p^3+{3\over 128}p^5+O(p^7)$$
Вычислим левую часть (5) при $$p_0=0,\!78$$, последовательно уточняя разложение внутреннего интеграла:
$$\begin{align*} &{1\over 0,\!78^2}\int\limits_0^{0,78}{p\over{\frac{1}{2}p}}\,dp=2,\!564102564,\\ &{1\over 0,\!78^2}\int\limits_0^{0,78}{p\over{\frac{1}{2}p+{1\over 16}p^3}}\,dp=2,\!501916372,\\ &{1\over 0,\!78^2}\int\limits_0^{0,78}{p\over{\frac{1}{2}p+{1\over 16}p^3+{3\over 128}p^5}}\,dp=2,\!493976851. \end{align*}$$
Хотя начальное значение параметра $$p_0=v_0/u_0=0,\!78$$ нельзя назвать малым, линеаризация по этому параметру дает погрешность менее 3%. Для линейного приближения ответ составил бы $$p_0=4/k=0,\!8\,$$. А учет кубической поправки уже дает погрешность меньше процента.