Хоккейная задача — 2

Продолжим решать «хоккейную задачу». В прошлом посте мы рассмотрели вариант задачи с искусственной поддержкой постоянной скорости вращения кольца. Перейдем теперь к варианту, когда за счет трения замедляется не только поступательное движение, но и вращение.

Напомним, что динамика кольца описывается уравнениями

$$\begin{align*} {du\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{u-v\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}},\\ {dv\over dt}&=-\int\limits_0^{2\pi}{d\alpha\over 2\pi}\,{v-u\sin\alpha\over\sqrt{u^2+v^2-2uv\sin\alpha}}, \end{align*}$$(1)

где $$v$$ — скорость поступательного движения, $$u=\omega R$$ — скорость вращательного движения кольца.

Система уравнений (1) симметрична относительно замены $$u$$ на $$v$$. Если в начальный момент $$u=v$$, то по соображениям симметрии это соотношение будет сохраняться между скоростями вплоть до остановки. Другой случай, который мы рассмотрим — это $$u>v$$. Противоположный случай $$u<v$$ будет вытекать из него простой заменой $$u$$ на $$v$$ из тех же соображений симметрии.

Вырожденный случай u = v

Оба уравнения системы принимают один и тот же вид

$${dv\over dt}=-\int\limits_0^{2\pi}{d\alpha\over 2\pi\sqrt2}\,\sqrt{1-\sin\alpha}={2\over\pi}.$$

Скорости совместного движения падают линейно со временем, но в $$\pi/2=1,\!57$$ раз медленнее отдельного вращения или отдельного поступательного движения.

Случай u > v

К сожалению, интегралы в системе (1) сводятся к эллиптическим, что не оставляет надежды решить систему аналитически. Остается численное решение.

Прямая попытка решить уравнение в Maple проваливается. Определенные интегралы заменяются нагромождением эллиптических интегралов, приводить которое здесь нет смысла. При построении графика мы видим сообщение об ошибке

Warning, cannot evaluate the solution past the initial point, problem may be complex, initially singular or improperly set up

Чтобы упростить выражения, накладываем ограничение $$u(t)\ge v(t)\ge 0$$ на каждый из интегралов.

sys_ode := {
    diff(u(t), t) = -`assuming`(
        [int(
            (u(t)-v(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
            alpha = 0 .. 2*Pi
        )],
        [u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
    )/(2*Pi),
    diff(v(t), t) = -`assuming`(
        [int(
            (v(t)-u(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
            alpha = 0 .. 2*Pi
        )],
        [u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
    )/(2*Pi), u(0) = 10, v(0) = 1
};

Ограничения устраняют сообщение об ошибке. Maple надолго задумывается, но выводит пустой график. Чтобы понять причину, выведем решение уравнения в какой-то точке.

p := dsolve(sys_ode, type = numeric):
p(1);

$$[t=1.,\\u(t)=10.9976102709142-2.84005015829721 10^{-8}{\rm I},\\v(t)=1.04887416587408+2.92542849266058 10^{-8}{\rm I}]$$

Накопление ошибки округления приводит к появлению ненулевой мнимой части в искомых функциях, из-за чего график пустой. Чтобы избежать появления мнимой части, возьмем в явном виде действительную часть правых частей уравнений:

sys_ode := {
    diff(u(t), t) = -Re(`assuming`(
        [int(
            (u(t)-v(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
            alpha = 0 .. 2*Pi
        )],
        [u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
    ))/(2*Pi),
    diff(v(t), t) = -Re(`assuming`(
        [Re(int(
            (v(t)-u(t)*sin(alpha))/sqrt(u(t)*u(t)+v(t)*v(t)-2*u(t)*v(t)*sin(alpha)),
            alpha = 0 .. 2*Pi
        )],
        [u(t) >= v(t) and v(t) >= 0, u(t) >= 0]
    ))/(2*Pi), u(0) = 10, v(0) = 1
};

Наконец, Maple, долго думая, всё же рисует график.

plots[odeplot](p, [
    [t, (10-t), color=gray],
    [t, sqrt(1-(1/10)*t), color=gray],
    [t, u(t), color = blue],
    [t, v(t), color = red]
], 0 .. 11);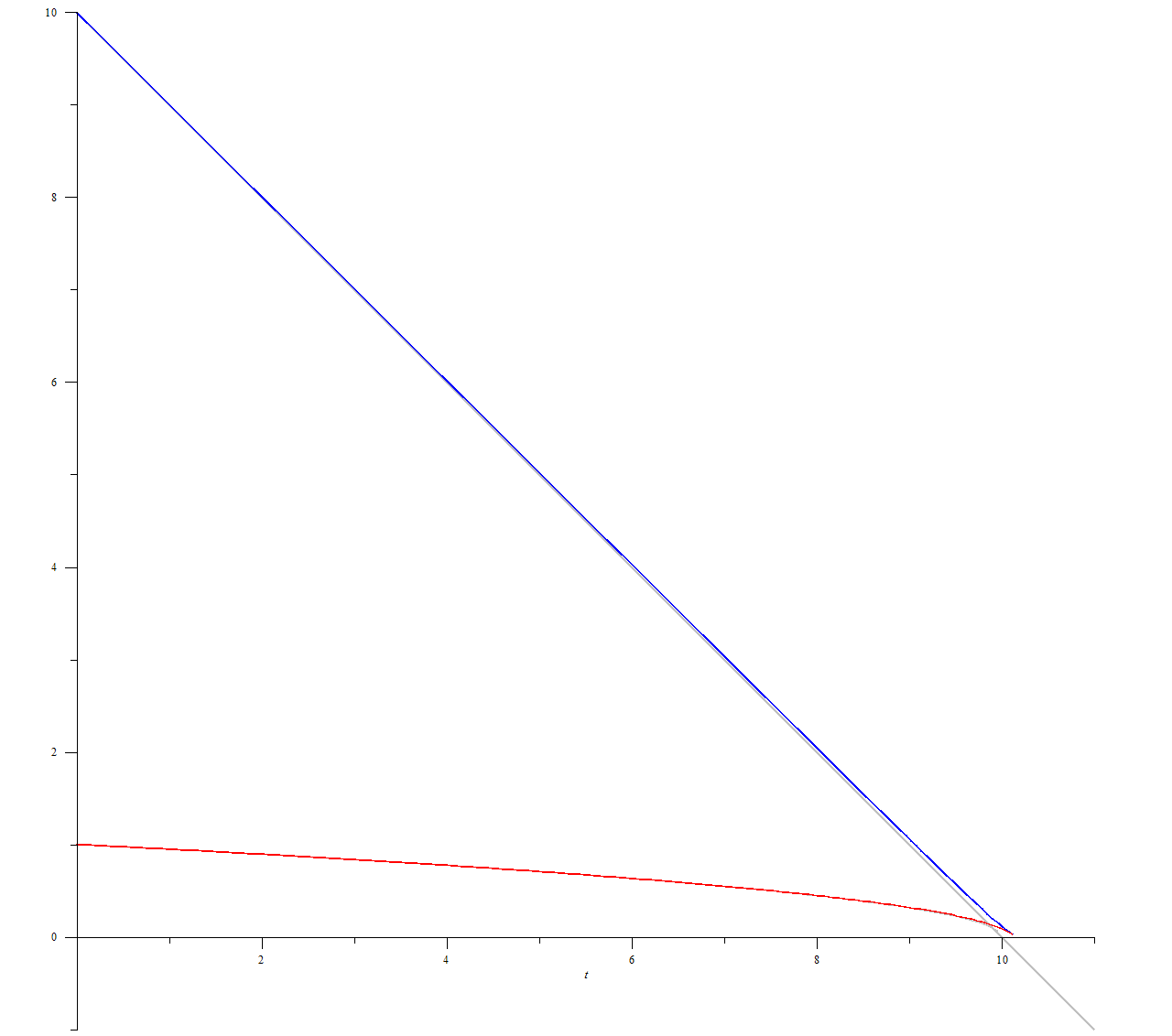

При этом мы видим предупреждение о точке остановки вычислений, которая, очевидно, совпадает с моментом окончания движения:

Warning, cannot evaluate the solution further right of 10.155665, probably a singularity

Для численного решения мы выбрали начальную поступательную скорость 1 и скорость вращения 10. Без вращения кольцо перемещается в течение 1 единицы времени на расстояние 0,5. Наличие вращения привело к тому, что поступательное движение сохранялось более 10 единиц времени.

Линеаризованное решение при u >> v

График $$u(t)$$ — синяя линия — практически совпадает с прямой. График $$v(t)$$ — красная линия — напоминает параболу. Такое поведение предсказывается линеаризованным решением в пределе $$u\gg v$$. Пренебрегая $$v$$ в первом уравнении системы (1) и раскладывая второе по степеням $$p=v/u$$, получаем

$$\begin{align*} {du\over dt}&=-1,\\ {dv\over dt}&=-{v\over 2u}. \end{align*}$$(2)

Решением этой системы являются функции $$u(t)=u_0-t$$, $$v(t)=v_0\sqrt{1-t/u_0}$$. Их графики изображены серыми линиями.

Как видим из численного решения и графика, приближение верно описывает характер движения, пока $$u$$ и $$v$$ не становятся сравнимыми. Вот график для случая, когда одна скорость в два раза больше другой:

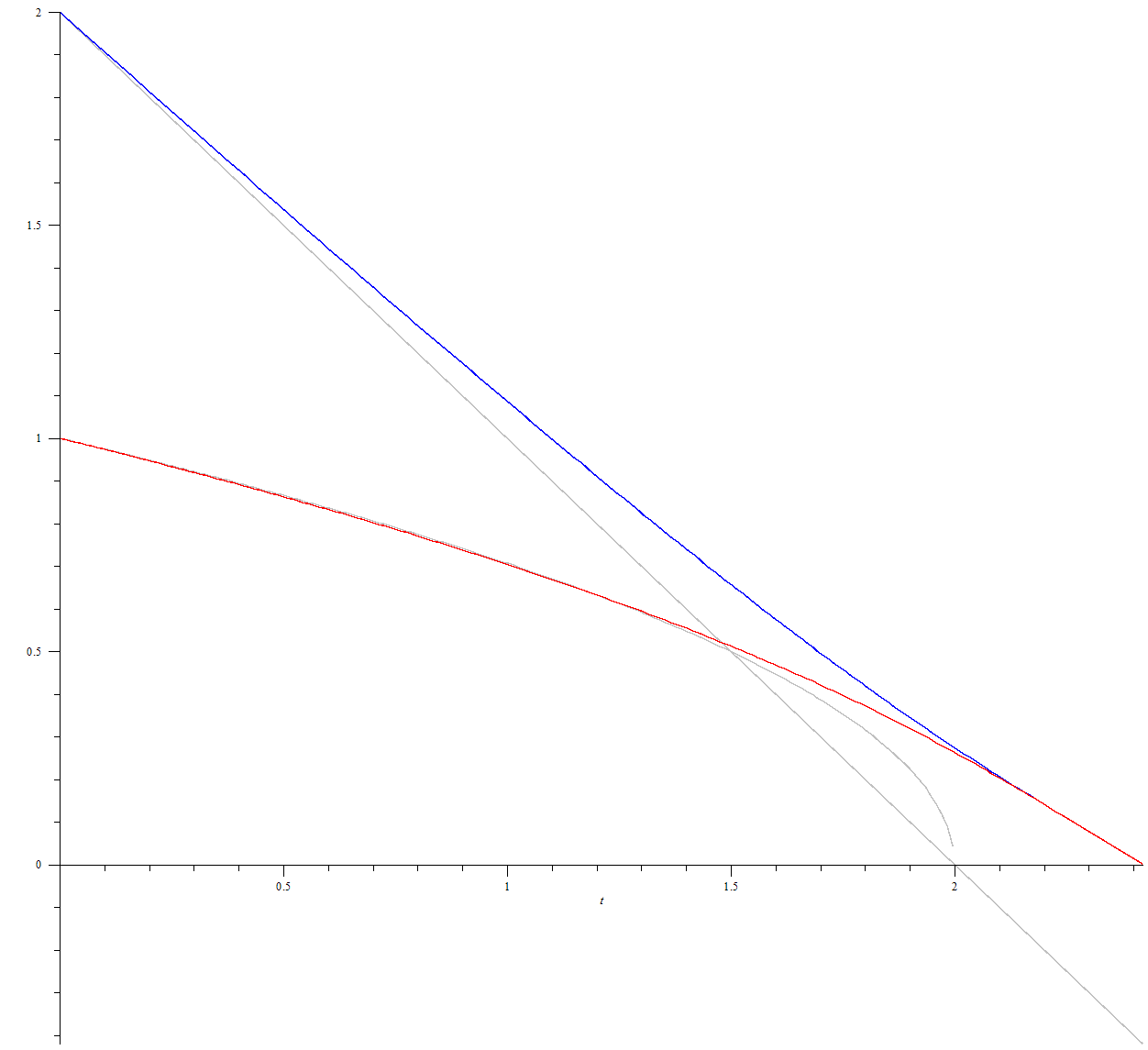
Здесь отличие от линеаризованного решения заметно практически сразу.

Путь до остановки: линеаризованное приближение

Пройденный кольцом путь дается площадью криволинейной трапеции под красной линией. В линеаризованном приближении криволинейная трапеция ограничена параболой и, как легко видеть, имеет площадь $$l=2u_0v_0/3$$. Если бы кольцо не вращалось, оно прошло бы расстояние $$l_0=v_0^2/2$$. Таким образом, чтобы увеличить проходимый путь в 5 раз, нужно закрутить кольцо с угловой скоростью

$$\omega_0={u_0\over R}={15\over 4}{v_0\over R}.$$

Напомним, что для прохождения кольцом того же пути при постоянном поддержании вращения его скорость должна быть в три раза меньше: $$\omega_0=(5/4)\,{v_0/R}$$.

Путь до остановки: численное решение

Теперь вычислим проходимый путь из первоначальных уравнений, без линеаризации.

Maple почему-то не нашел точку остановки («сингулярности») для начального значения 15/4 и некорректно продолжил решение. Приближенное положение этой точки находим подбором.

dsol2p := dsolve(sys_ode, type = numeric, output = listprocedure):
v := eval(v(t), dsol2p):
v(4.04);

$$0.00664275658541608$$

v(4.05);

$$0.000276558860981139$$

v(4.06);

$$0.00946581059191108$$

int(v(t), t = 0 .. 4.05);

$$2.5535588257745343$$

Последний результат Maple вычислял больше 10 минут. Как видим, для начального значения 15/4 погрешность линеаризованного приближения составляет 2%.

Вывод

Мы решили «хоккейную задачу» в исходной упрощенной формулировке и без упрощений в линеаризованном приближении. С помощью системы компьютерной алгебры Maple убедились, что для условия этой задачи линеаризованное приближение дает ошибку на несколько процентов.