Круговая трактриса
Я люблю задачки, в которых нужно искать траектории частиц или уравнения необычных линий. К сожалению, они не всегда решаются аналитически. Разберем задачу, у которой аналитическое решение существует.
Задача
По окружности небольшого радиуса едет трактор. К нему на жестком стержне прикреплен груз (например, прицеп). По какой траектории будет двигаться груз?
При движении трактора по прямой траектория груза известна — это трактриса. В нашем случае движение будет более сложным. Я сделал анимацию искомой траектории — круговой трактрисы. Посмотрите на эту красоту.
Решение
Будем считать трактор точкой, движущейся по окружности радиуса r, и обозначать на рисунках зеленым кружком. К нему с помощью стержня длины L прикреплен груз (красный кружок).
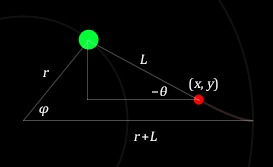
Из кинематических связей координаты груза определяются формулами
$$x=r\cos\varphi+L\cos\theta,\quad y=r\sin\varphi+L\sin\theta.$$
Еще одна кинематическая связь дает ограничение на скорость груза. По условию вектор скорости всегда направлен на трактор. Поэтому угол θ в прямоугольном треугольнике совпадает с точностью до знака с углом наклона касательной:
$${dy\over dx}=\text{tg\,}\theta.$$
Мы выразим θ через φ и получим уравнение траектории в параметрической форме. Введем новый параметр β = L/r, возьмем дифференциалы первых двух уравнений и подставим в последнее:
$$-{\cos\varphi\,d\varphi+\beta\cos\theta\,d\theta\over \sin\varphi\,d\varphi+\beta\sin\theta\,d\theta}=\text{tg\,}\theta.$$
Приведя к общему знаменателю и воспользовавшись основным тригонометрическим тождеством и формулой косинуса разности, получаем дифференциальное уравнение
$$\beta{d\theta\over d\varphi}+\cos(\theta-\varphi)=0.$$
Оно решается разделением переменных после замены θ = α + φ. Решение имеет разный вид в зависимости от параметра β:
$$\theta(\varphi)=\left\{\begin{array}{l}\varphi-2\,\text{arctg}\left[\sqrt{\dfrac{\beta+1}{\beta-1}}\,\text{tg}\left(\varphi\,\dfrac{\sqrt{\beta^2-1}}{2\beta}\right)\right],\quad\beta>1,\\\vphantom{\dfrac{1}{1}}\varphi-2\,\text{arctg}\,\varphi,\quad\beta=1,\\\varphi-2\,\text{arctg}\left[\sqrt{\dfrac{1+\beta}{1-\beta}}\,\text{th}\left(\varphi\,\dfrac{\sqrt{1-\beta^2}}{2\beta}\right)\right],\quad\beta<1.\end{array}\right.$$
Анализ решения
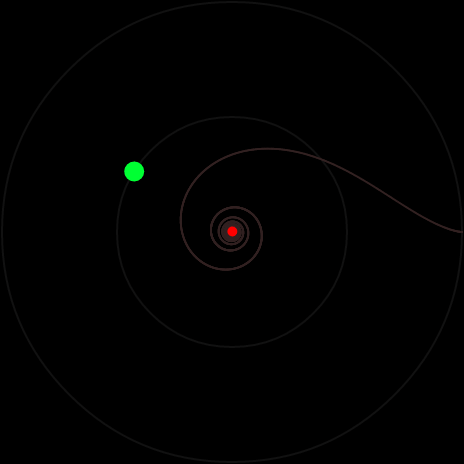
Если β < 1, движение непериодическое. Груз следует за трактором, асимпотически приближаясь к окружности. Интересный режим возникает при β = 1. Тогда груз неограниченно приближается к центру окружности:
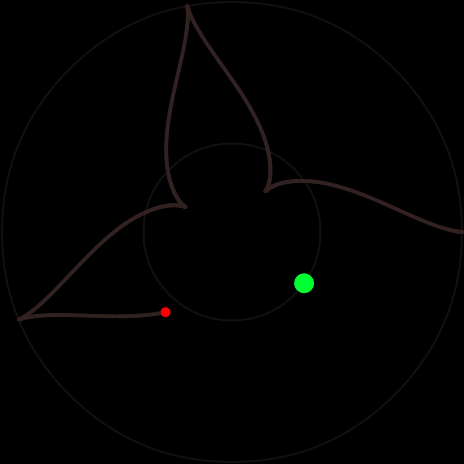
Если β > 1, движение будет периодическим по звездообразной траектории:
Чтобы найти угол между направлениями на соседние максимум и минимум, заметим, что груз находится дальше всего от центра, когда θ и φ совпадают, и ближе всего к центру, когда отличаются на π. В первом случае тангенс равен нулю, во втором — расходится. Возьмем направление на максимум θ = φ = 0 и направление на первый минимум φ = θ + π, определяющийся условием
$$(\pi+\theta)\,{\sqrt{\beta^2-1}\over 2\beta}={\pi\over 2}.$$
Угол между направлениями составляет
$$\theta=\pi\left({\beta\over\sqrt{\beta^2-1}}-1\right).$$
Если параметр удовлетворяет условию
$${1\over N}={\beta\over\sqrt{\beta^2-1}}-1,$$
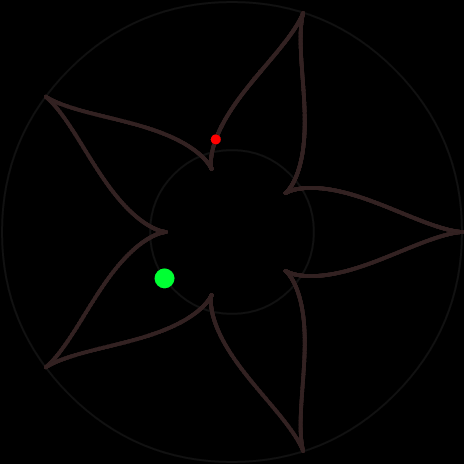
то груз описывает замкнутую линию — N-конечную звезду. Вот пример для $$N=5,\beta=6/\sqrt{11}$$:
Торможение реликтовым излучением
На втором курсе за неделю перед досрочным экзаменом по теоретической физике Семен Соломонович Герштейн задал мне две задачи. В одной требовалось найти угловое распределение синхротронного излучения электрона, движущегося по окружности. Вторая оказалась интереснее: найти силу торможения со стороны реликтового излучения на площадку, движущуюся перпендикулярно самой себе. Остановимся на ней подробнее. Записей с тех времен у меня не сохранилось, а в литературе опубликованы противоречивые результаты. Хороший повод заново разобраться в задаче.
Обозначения и соглашения
Под реликтовым излучением мы подразумеваем равновесное тепловое излучение при некоторой температуре T. Напомним, что плотность энергии и давление равновесного излучения определяются температурой: ε = 4πσT4/c, P = ε/3.
В системе отсчета, связанной с реликтовым излучением, оно однородно и изотропно. Относящиеся к ней величины будем обозначать символами без штрихов. Относительно этой системы со скоростью v движется площадка (например, диск) с коэффициентом отражения R. Штрихами обозначим величины в сопутствующей системе отсчета (связанной с площадкой).
Будем опускать скорость света c в тех формулах, где она легко восстанавливается из соображений размерности.
Обзор литературы
В публикациях по этой проблеме нет консенсуса. Например, в письме Андрея Шепелева в УФН под названием «Космический микроволновой фон и аристотелевы представления о движении» приведена формула для давления на площадку $$P=-v\,(1+v^2/2)\,\varepsilon/2$$. Этот ответ, как мы увидим ниже, явно ошибочен. Автор не раскрывает вычислений, поэтому невозможно понять, где ошибка.
В работе Баласаняна и Мкртчяна «Blackbody radiation drag on a relativistically moving mirror» вычисляется плотность импульса в системе отсчета, связанной с диском, и она отождествляется с давлением (с точностью до учета отражения). По поводу этой работы у меня есть два замечания.
$$n'(\vec{k}')={1\over e^{\gamma(\omega' +k'_xv)/T}-1}.$$(1)
В то же время плотность импульса электромагнитного излучения отличается на множитель 1/c2 от вектора Поинтинга, проекции которого есть компоненты T0i тензора
$$T^{\mu\nu}=\begin{pmatrix}\varepsilon &0&0&0\\0&\varepsilon/3&0&0\\0&0&\varepsilon/3&0\\0&0&0&\varepsilon/3\end{pmatrix},$$
сразу получаем плотность импульса (см. II том Ландау и Лифшица, §35, формула 35.3)
$$S'_x=-{4\over 3}\,\varepsilon\,{v\over 1-v^2}.$$(2)
Вычисление в сопутствующей системе отсчета
Давление как силу на единицу поверхности определим через импульс, передаваемый диску при отражении или поглощении фотонов за единицу времени:
$$P={F\over S}={1\over S}{\hbar\Delta k\over\Delta t}.$$
Если фотоны летят под углом θ к нормали, то за время Δt до неподвижной площадки S долетят фотоны из объема S cΔt |cos θ|. Из них доля R отразится и доля (1−R) поглотится. Каждый поглощенный фотон отдаст импульс $$\hbar k\cos\theta=\hbar\omega\cos\theta/c$$, а каждый отраженный — в два раза больше. Собирая всё вместе, получаем в сопутствующей системе отсчета
$$P=\int{\hbar\omega'\cos\theta'\over S\,c\Delta t'}\,(1+R)\,S\,c\Delta t'\,|\cos\theta'|\,n'(\vec{k}')\,d^3k'.$$
Напомним, что частота ω и волновой вектор $$\vec{k}$$ образуют четырехвектор $$(\omega, \vec{k})$$. Переход к движущейся системе координат осуществляется преобразованиями Лоренца
$$\omega'={\omega-k_xv\over\sqrt{1-v^2}},\qquad k_x'={k_x-\omega v\over\sqrt{1-v^2}}.$$
Функция распределения $$n(\vec{k})$$ в фазовом пространстве инвариантна относительно преобразований Лоренца, так как и элемент фазового объема $$d^3r\,d^3k$$, и число частиц $$dN=n(\vec{r},\vec{k})\,d^3r\,d^3k$$ есть инварианты (подробнее см. II том Ландау и Лифшица, §10). Именно поэтому функция распределения в движущейся системе $$n'(\vec{k'})=n(\vec{k})$$ есть обычное распределение Бозе — Эйнштейна (1), в которое подставлена преобразованная частота.
В итоге давление определяется следующим интегралом
$$P=\int \hbar\omega'\cos\theta'\,(1+R)\,|\cos\theta'|\,{const\over exp\left(\dfrac{\hbar\omega'}{kT}\,\dfrac{1+v\cos\theta'}{\sqrt{1-v^2}}\right)-1}\,\omega'^2\,d\omega'\,{d(\cos\theta')\over 2}.$$(3)
Вместо того чтобы следить за комбинацией констант, которая в итоге должна свестись к постоянной
$$\varepsilon=\int \hbar\omega\,{const\over exp\left(\dfrac{\hbar\omega}{kT}\right)-1}\,\omega^2\,d\omega={4\pi\sigma\over c}T^4.$$
Еще отсюда видно, что (3) можно упростить, проинтегрировав по частотам. Множитель $${\sqrt{1-v^2}}/{(1+v\cos\theta')}$$ перед температурой в экспоненте появится под интегралом в четвертой степени. Дальнейшее вычисление тривиально:
$$P=\varepsilon\,(1+R)\int\limits_{-1}^{1}\cos\theta'\,|\cos\theta'|\,\dfrac{(1-v^2)^2}{(1+v\cos\theta')^4}\,{d(\cos\theta')\over 2},$$
$${\Large\boxed{P=-\varepsilon\,(1+R)\,\frac{v\,(1+v^2/3)}{1-v^2}}.}$$(4)
Чтобы убедиться в правильности результата, вычислим тем же методом давление фотонного газа на одну сторону покоящейся пластины. Зависящий от скорости подынтегральный множитель исчезает, а интеграл в пределах от 0 до 1 равен 1/3. Полное давление есть (1+R) ε/6. Если пластина всё отражает и ничего не поглощает, давление совпадает с ожидаемой величиной ε/3. Если пластина всё поглощает, давление равно ε/6 и составляет половину от давления фотонного газа ε/3. Вторая половина набегает за счет собственного излучения пластины, которое мы в наших расчетах не учитывали.
Формула (4) не совпадает ни с результатом Шепелева, который утверждает, что ответ сложен, и раскладывает его в ряд, ни с результатом Баласаняна, который ошибочно отождествляет в этой задаче плотность импульса и давление.
Вычисление в неподвижной системе отсчета
Тот же результат получается и в неподвижной системе отсчета. В ней не нужно иметь дела с функцией распределения фотонов, однако
$$\dvisvgm\usetikzlibrary{decorations.pathmorphing} \begin{tikzpicture}[line width=0.2mm,scale=1.0545]\small \tikzset{>=stealth} \tikzset{snake it/.style={->,semithick, decoration={snake,amplitude=.3mm,segment length=2.5mm,post length=0.9mm},decorate}} \def\h{3} \def\d{0.2} \def\ww{1.4} \def\w{1+\ww} \def\p{1.5} \def\r{0.7} \draw[opacity=0, use as bounding box] (-0.40,-0.12) rectangle (2.60,4.94); \coordinate[label=below:$A_1$] (A1) at (\ww,\p); \coordinate[label=above:$B_1$] (B1) at (\ww,\p+\h); \coordinate[label=below:$A_2$] (A2) at (\w,\p); \coordinate[label=above:$B_2$] (B2) at (\w,\p+\h); \coordinate[label=left:$C$] (C1) at (0,0); \coordinate[label=left:$D$] (D) at (0,\h); \draw[fill=blue!14](A2)--(B2)-- ++(\d,0)-- ++(0,-\h)--cycle; \draw[gray,thin](C1)-- +(\w+\d,0); \draw[dashed,gray,fill=blue!5](A1)-- (B1)-- ++(\d,0)-- ++(0,-\h)-- cycle; \draw[dashed,line width=0.14mm](A1)--(C1)--(D)--(B1); \draw[snake it](C1)--(A2) node[pos=0.6,below] {$c\Delta t$}; \draw[->,semithick](\ww,\p+0.44*\h)-- +(\w-\ww,0) node[pos=0.6,above] {$v\Delta t$}; \draw[snake it](D)--(B2); \draw[thin](\r,0) arc (0:atan2(\p,\w):\r) node[midway,right,yshift=0.06cm] {$\theta$}; \end{tikzpicture}$$ $$\dvisvgm\usetikzlibrary{decorations.pathmorphing} \usetikzlibrary{animations} \newcommand{\mycharge}[1][]{ \fill[green!50!black] (#1) circle (0.5mm); } \begin{tikzpicture}[line width=0.2mm,scale=1.0545]\small \tikzset{>=stealth} \tikzset{snake it/.style={->, decoration={snake,amplitude=.3mm,segment length=2.5mm,post length=0.9mm},decorate} } \def\h{3} \def\d{0.2} \def\ww{1.4} \def\ds{1} \def\w{\ds+\ww} \def\p{1.5} \def\r{0.7} \draw[opacity=0, use as bounding box] (-0.40,-0.12) rectangle (2.60,4.94); \coordinate[label=below:$A_1$] (A1) at (\ww,\p); \coordinate[label=above:$B_1$] (B1) at (\ww,\p+\h); \coordinate[label=below:$A_2$] (A2) at (\w,\p); \coordinate[label=above:$B_2$] (B2) at (\w,\p+\h); \coordinate[label=left:$C$] (C1) at (0,0); \coordinate[label=left:$D$] (D) at (0,\h); \draw[dashed,gray,fill=blue!5](A1)-- (B1)-- ++(\d,0)-- ++(0,-\h)-- cycle; \draw[gray,snake it](C1)--(A2); \draw[gray,snake it](D)--(B2); \begin{scope} :shift = { 0s = "{(0,0)}", 1s = "{(0,0)}", 4s = "{(\w,\p)}", 5s = "{(\w,\p)}", repeats} \foreach \x in {0,0.52,...,3} { \begin{scope} :opacity = {0s = "1", 3.9-\x s = "1", 3.92-\x s="0", 5s="0", repeats } \foreach \y in {0,0.5,...,\h} { \mycharge[\x*\ww/3,\y+\x*\p/3]; } \end{scope} } \end{scope} \begin{scope} :shift = { 0s = "{(0,0)}", 1s = "{(0,0)}", 4s = "{(\ds,0)}", 5s = "{(\ds,0)}", repeats} \draw[fill=blue!14](A1)-- (B1)-- ++(\d,0)-- ++(0,-\h)-- cycle; \end{scope} \draw[gray,thin](C1)-- +(\w+\d,0); \draw[dashed,line width=0.14mm](A1)--(C1)--(D)--(B1); \draw[thin](\r,0) arc (0:atan2(\p,\w):\r) node[midway,right,yshift=0.06cm] {$\theta$}; \end{tikzpicture}$$
Чтобы понять, сколько летящих под углом θ фотонов с частотой ω попадет за время Δt на площадку AB, нужно ввести понятие «заметаемого объема» (объем, фотоны из которого попадут на диск) и умножить его величину на плотность фотонов nω. За это время площадка переместится из положения A1B1 в положение A2B2, а фотоны из точек C и D долетят до диска. Таким образом, заметаемый объем соответствует фигуре A1B1DС, и его величина равна S |cΔt cos θ − vΔt|.
При отражении фотона от площадки в сопутствующей системе отсчета знак проекции волнового вектора фотона изменяется на противоположный: $$k'_{2x}=-k'_{1x}$$. Найдем соответствующее изменение в неподвижной системе:
$$\begin{aligned}\Delta k &=k_{1x}-k_{2x}=k_{1x}-\gamma(k'_{2x}+\omega'_2v)=k_{1x}+\gamma(k'_{1x}-\omega'_1v)=\\&=k_{1x}+\gamma\left(\gamma(k_{1x}-\omega_1 v)-\gamma(\omega_1-k_{1x}v)v\right)=k_{1x}+\gamma^2\left(k_{1x}(1+v^2)-2v\omega\right).\end{aligned*}$$
Выражая проекцию волнового вектора через частоту фотона и азимутальный угол $$k_x=\omega\cos\theta$$, получаем
$$\Delta k=\omega\left[\cos\theta\left(1+{1+v^2\over 1-v^2}\right)-2{v\over 1-v^2}\right]={2\omega\over 1-v^2}\,(\cos\theta-v).$$
Ясно, что двойку в последнем выражении нужно заменить на (1+R), чтобы учесть случай произвольного коэффициента отражения R. Давление
$$P_\omega=\int{\hbar\omega\over S\,c\Delta t}\,{1+R\over 1-v^2}\,(\cos\theta-v)\,S|c\Delta t\cos\theta-v\Delta t|\,n_\omega\,{d(\cos\theta)\over2},$$
$$P_\omega={n_\omega\over 2}\hbar\omega\,{1+R\over 1-v^2}\int\limits_{-1}^{1}dx\,(x-v)|x-v|.$$
После вычисления интеграла и усреднения плотности энергии $$n_\omega\hbar\omega$$ по частотам получается формула (4).
Метод наименьших квадратов во многомерном пространстве
Я собираюсь применить метод наименьших квадратов для проведения гиперплоскости через набор точек во многомерном пространстве. Для начала вспомним суть метода и поймем, в чем состоит задача.
В простейшем случае метод наименьших квадратов применяется для проведения прямой линии через набор экспериментальных точек и состоит в минимизации суммы квадратов отклонений $$\inline\sum(y_i-ax_i-b)^2$$, которые списываются на погрешность измерений. В результате минимизации для коэффициентов a и b получается простая система линейных уравнений. Здесь важно предположение о том, что ошибки по оси x пренебрежимо малы по сравнению с ошибками по оси y. Если это не так, то минимизировать нужно более сложное выражение.
Иногда возникает задача другого рода — провести геометрическую прямую через набор геометрических точек «наилучшим образом». Для этой задачи метод наименьших квадратов нужно адаптировать, так как поспешное применение формул для коэффициентов a и b будет давать разные прямые в разных системах координат. Теперь отклонения по осям должны давать одинаковый вклад. Правильный подход заключается в минимизации суммы квадратов расстояний $$\inline\sum(y_i-ax_i-b)^2/(1+a^2)$$ от точек (xi, yi) до проводимой прямой. Он дает нелинейную систему уравнений, которую можно решать численно. Однако этот подход тяжело обобщается на интересующий меня многомерный случай. Поэтому мы с самого начала будем рассматривать задачу во многомерном пространстве.
Задача
Пусть задан набор точек $$\vec{x}^k$$. Мы хотим провести гиперплоскость $$(\vec{n}\cdot\vec{x}) = d$$ такую, что сумма квадратов расстояний от точек $$\vec{x}^k$$ до нее будет минимальна. Расстояние до гиперплоскости находится с помощью проекции на единичный вектор нормали $$\vec{n}$$, и выражение для минимизации принимает вид
$$\sum_k\left((\vec{n}\cdot\vec{x}^k)-d\right)^2\to\text{min}.$$
При этом нужно учитывать уравнение связи $$(\vec{n}\cdot\vec{n}) = 1$$, которое уменьшает на 1 количество степеней свободы в неизвестных величинах ni, d. Учет связи выполняется с помощью метода множителей Лагранжа. Однако мы пойдем другим путем, который сократит выкладки и напрямую приведет к выражениям, подходящим для численного счета. Мы разрешим вектору $$\vec{n}$$ иметь произвольную длину, и введем явную нормировку:
$$\sum_k\left({(\vec{n}\cdot\vec{x}^k)\over|\vec{n}|}-d\right)^2\to\text{min}.$$
Параллельный перенос
Продифференцируем по d:
$$\sum_k\left({(\vec{n}\cdot\vec{x}^k)\over|\vec{n}|}-d\right)={(\vec{n}\cdot\sum_k\vec{x}^k)\over|\vec{n}|}-\sum_kd=0.$$
Как видим, «центр масс» набора точек $$\inline\sum\vec{x}^k/\sum 1$$ находится на искомой плоскости. Выполним параллельный перенос системы координат таким образом, чтобы ее начало совпало с центром набора точек $$\inline\sum\vec{x}^k=0$$. В этой системе координат d=0.
Условие на вектор нормали
Перейдем к индексным обозначениям и продифференцируем по na:
$${\partial\over\partial n_a}\left({n_ix_i^k\,n_jx_j^k\over n_ln_l}\right)={2x_a^k\,n_jx_j^k\over n_ln_l}-{2n_a\,n_ix_i^k\,n_jx_j^k\over n_ln_l\,n_pn_p}=0,$$
$$n_jx_j^k\left[x_a^k(n_pn_p)-n_a(n_ix_i^k)\right]=0,$$
$$\sum_k\vec{n}\cdot\vec{x}^k\left[\vec{x}^k(\vec{n}\cdot\vec{n})-\vec{n}(\vec{n}\cdot\vec{x}^k)\right]=0.$$
Вычислительный аспект
Нелинейное уравнение относительно вектора $$\vec{n}$$ можно решать методом итераций:
$$\sum_k\vec{n}_{i+1}\cdot\vec{x}^k\left[\vec{x}^k(\vec{n}_i\cdot\vec{n}_i)-\vec{n}_i(\vec{n}_i\cdot\vec{x}^k)\right]=0.$$
С помощью матрицы $$A_{aj}(\vec{n})=\left[x_a^k(n_pn_p)-n_a(n_ix_i^k)\right]x_j^k$$ оно представляется в виде
$$A(\vec{n}_i)\,\vec{n}_{i+1}=0$$
и сводится к поиску ядра линейного оператора. Нетривиальность ядра связана с «лишней» степенью свободы, появившейся
По теореме Фредгольма ядро оператора ортогонально образу сопряженного оператора, то есть линейной оболочке, натянутой на строки $$\vec{a}_a$$ матрицы $$A_{aj}(\vec{n}_i)$$. Алгоритм поиска ортогонального дополнения состоит в выборе произвольного вектора $$\vec{r}$$ и ортогонализации набора векторов $$\vec{r}, \vec{a}_a$$:
$$\vec{r}^{\,\prime}=\vec{r}-\vec{a}_1{(\vec{r}\cdot\vec{a}_1)\over(\vec{a}_1\cdot\vec{a}_1)},$$
$$\vec{a}_2^{\,\prime}=\vec{a}_2-\vec{a}_1{(\vec{a}_2\cdot\vec{a}_1)\over(\vec{a}_1\cdot\vec{a}_1)},\quad\vec{r}^{\,\prime\prime}=\vec{r}^{\,\prime}-\vec{a}_2^{\,\prime}{(\vec{r}^{\,\prime}\cdot\vec{a}_2^{\,\prime})\over(\vec{a}_2^{\,\prime}\cdot\vec{a}_2^{\,\prime})}\ldots$$
Так как строки матрицы $$A(\vec{n}_i)$$ линейно зависимы, один из векторов $$\vec{a}_a$$ при ортогонализации из набора исключается. Для большей определенности алгоритма в качестве начального приближения перебираем базисные векторы, пока в результате ортогонализации не получится ненулевой вектор следующего приближения $$\vec{n}_{i+1}$$. В двумерном и трехмерном случае процесс ортогонализации значительно упрощается. Например, в трехмерном случае нетривиальный элемент ядра найдется среди тройки векторов $$\vec{a}_1\times\vec{a}_2, \vec{a}_1\times\vec{a}_3, \vec{a}_2\times\vec{a}_3$$.
Как показывают практические вычисления, последовательные приближения $$\vec{n}_i$$ быстро сходятся к искомому вектору нормали.
Магнитные монополи, потоки энергии и квантование заряда
Мы уже рассчитывали замкнутые потоки энергии в стационарных полях зарядов и магнитов. Перейдем к более экзотическому примеру с участием не открытого на опыте магнитного монополя.
Как и в любых скрещенных электрических и магнитных полях, вокруг электрического заряда и магнитного монополя существуют потоки энергии, определяемые вектором Пойнтинга $$\vec{S}\sim\vec{E}\times\vec{B}$$. Они замкнуты и охватывают ось симметрии системы, что может означать наличие в ней момента импульса.
Если заряд движется строго на монополь, то взаимодействие между ними отсутствует. Действительно, монополь не испытывает действие электрического поля заряда. Магнитное поле заряда на линии движения нулевое. Монополь не создает электрическое поле, а его магнитное поле коллинеарно скорости заряда, поэтому силы на заряд тоже не действуют. Отсутствие взаимодействия в этом случае наводит на мысль о том, что момент импульса остается неизменным.
Есть и другое качественное рассуждение в пользу неизменности момента импульса. По соображениям размерности момент импульса, как безразмерная величина (в единицах c = ħ = 1), не может зависеть от расстояния между зарядом и монополем — единственного размерного параметра системы. Убедимся в этом непосредственным вычислением.
Поместим электрический заряд q в точку $$\vec{a}$$ и магнитный заряд m в точку $$-\vec{a}$$. Тогда они будут создавать поля
$$\vec{E}(\vec{R})={q\over |\vec{R}-\vec{a}|^3}(\vec{R}- \vec{a}),\quad\vec{B}(\vec{R}) ={m\over |\vec{R} + \vec{a}|^3}(\vec{R} + \vec{a}).$$
Плотность импульса связана с вектором Пойнтинга
$$\vec{P} = {\vec{S} \over c^2} = {1\over 4\pi c}\vec{E}\times\vec{B}= {qm\over 4\pi c}{(\vec{R}-\vec{a})\times (\vec{R}+\vec{a})\over \left(\left(R^2+a^2\right)^2-4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$
Полный момент импульса находится интегрированием по всему пространству
$$\vec{L}=\int\!\vec{R}\times\vec{P}\,dV={qm\over 2\pi c}\int\! dV{\vec{R}\times[\vec{R}\times\vec{a}]\over \left(\left(R^2 + a^2\right)^2- 4\left(\vec{R}\cdot\vec{a}\right)^2\right)^{3/2}}.$$
Выбираем ось z вдоль $$\vec{a}$$, угол между этой осью
$$L_z={qm\over c}\int\limits_0^{\infty}\! R^2dR\int\limits_{-1}^{1}\! d(\cos\theta){-a\,R^2\sin^2\theta\over \left(\left(R^2 + a^2\right)^2- 4(R\,a\cos\theta)^2\right)^{3/2}}.$$
Разделим числитель и знаменатель на a6 и введем новую безразмерную переменную интегрирования r = R/a. Таким образом, мы избавились от явной зависимости момента импульса от расстояний. Двойной интеграл не зависит от параметров задачи. С помощью любимого математического пакета можно убедиться, что он равен 1.
$$L_z=-{qm\over c}\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! d(\cos\theta){1-\cos^2\theta\over \left(\left(r^2 + 1\right)^2- 4r^2\cos^2\theta\right)^{3/2}}=-{qm\over c}.$$
Таким образом, момент импульса в системе заряда и монополя направлен к последнему и равен (с точностью до несущественного множителя c) произведению их величин.
В квантовой механике момент импульса квантуется. Из полуклассических соображений приравнивая полученное выше выражение для момента к минимальному значению ħ/2, мы получаем такое же ограничение на минимальные («элементарные») значения электрического и магнитного зарядов, как и в теории Дирака (где ограничение следует из дискретности прироста фазы волновой функции заряда при полном обороте вокруг монополя)
$$q_{min}\, m_{min}={\hbar c\over 2}.$$
Как видим, присутствие во Вселенной хотя бы одного монополя приводит к квантованию всех электрических зарядов.
В завершение потренируемся в технике вычисления интегралов. Обозначим искомый интеграл через $$I$$:
$$I=\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! dz{1-z^2\over \left(\left(r^2 + 1\right)^2- 4r^2z^2\right)^{3/2}}=\int\limits_0^{\infty}\! r^4dr\int\limits_{-1}^{1}\! dz{1-z^2\over \left(\left(r^2 - 1\right)^2+4r^2- 4r^2z^2\right)^{3/2}}.$$
Рассмотрим вспомогательный интеграл $$J(b)$$, дополнительно зависящий от некоторого параметра $$b$$:
$$J(b)=\int\limits_{-1}^{1}{dz\over \sqrt{\left(r^2 - 1\right)^2+ 4b^2r^2\left(1-z^2\right)}}.$$
Вычислим $$J'(b)$$:
$$J'(b)=\int\limits_{-1}^{1}{dz\over \sqrt{\left(r^2 - 1\right)^2+ 4b^2r^2\left(1-z^2\right)}^3}\cdot\left(-{1\over 2}\right)8br^2\left(1-z^2\right).$$
$$J'(1)$$ с точностью до коэффициента совпадает с внутренним интегралом в $$I$$. Сравнивая их, можем записать:
$$I=\int\limits_0^{\infty}\! r^2dr\cdot{-J'(1)\over 4}.$$
Упростим и вычислим $$J(b)$$, введя константы $$A=\left(r^2 - 1\right)^2$$ и $$B=4b^2r^2$$:
$$\begin{align*}&\int\limits_{-1}^{1}{dz\over \sqrt{A+B\left(1-z^2\right)}}={2\over\sqrt{B}}\int\limits_{0}^{1}{dz\over\sqrt{{A\over B}+1-z^2}}= \begin{vmatrix} z=\sqrt{{A\over B}+1}\sin\varphi\\ dz=\sqrt{{A\over B}+1}\cos\varphi\ d\varphi \\ \end{vmatrix}=\\ &={2\over\sqrt{B}}\int\limits_{0}^{\arcsin\left(1/\sqrt{{A\over B}+1}\right)}{\sqrt{{A\over B}+1}\cos\varphi\ d\varphi\over\sqrt{{A\over B}+1-\left({A\over B}+1\right)\sin^2\varphi}}= {2\over\sqrt{B}}\int\limits_{0}^{\arcsin\sqrt{B\over A+B}}d\varphi=\\ &={2\over\sqrt{B}}\arcsin\sqrt{B\over A+B}={2\over\sqrt{B}}\arctg\sqrt{B\over A}. \end{align*} $$
Возвращаемся к исходным переменным:
$$\begin{align*}J'(b)&={d\over db}\left({2\over\sqrt{4b^2r^2}}\arctg\sqrt{4b^2r^2\over \left(r^2 - 1\right)^2}\right)= {d\over db}\left({1\over br}\arctg{2br\over \left|r^2 - 1\right|}\right)=\\ &=-\frac{1}{b^2 r}\arctg\dfrac{2rb}{|r^2 - 1|} +\frac{1}{br \left(1+ \dfrac{4r^2 b^2}{|r^2 - 1|^2}\right)}{2r\over |r^2 - 1|}. \end{align*}$$
Подставляем $$b=1$$ и упрощаем:
$$\begin{align*}J'(1)&=-\frac{1}{r}\arctg\dfrac{2r}{|r^2 - 1|} +\frac{2|r^2 - 1|}{\left(r^2 - 1\right)^2+ {4r^2}}. \end{align*}$$
Возвращаемся к первоначальному интегралу, разбиваем на сумму интегралов на интервалах $$(0,1)$$ и $$(1,\infty)$$, чтобы раскрыть модули. Также выполняем замену переменных $$r=1/u$$ в первом из них и группируем в виде общего интеграла:
$$\begin{align*} I&=\int\limits_0^{\infty}\! dr\left(\frac{r}{4}\arctg\dfrac{2r}{|r^2 - 1|}-\frac{r^2|r^2 - 1|}{2\left(\left(r^2 - 1\right)^2+ {4r^2}\right)}\right)=\\ &=\int\limits_0^{1}\! dr\left(\frac{r}{4}\arctg\dfrac{2r}{1-r^2}-\frac{r^2(1-r^2)}{2\left(\left(r^2 - 1\right)^2+ {4r^2}\right)}\right)+\\ &\qquad\qquad+\int\limits_1^{\infty}\! dr\left(\frac{r}{4}\arctg\dfrac{2r}{r^2 - 1}-\frac{r^2(r^2 - 1)}{2\left(\left(r^2 - 1\right)^2+ {4r^2}\right)}\right)=\\ &=\int\limits_\infty^{1}\! -{du\over u^2}\left(\frac{1}{4u}\arctg\dfrac{2/u}{1-1/u^2}-\frac{(1/u)^2(1-1/u^2)}{2\left(\left(1/u^2 - 1\right)^2+ 4/u^2\right)}\right)+ \int\limits_1^{\infty} dr\ldots=\\ &=\int\limits_1^{\infty}\! {du\over u^4}\left(\frac{u}{4}\arctg\dfrac{2u}{u^2-1}-\frac{u^2(u^2-1)}{2\left(\left(1-u^2 \right)^2+ 4u^2\right)}\right)+ \int\limits_1^{\infty}\! dr\ldots=\\ &=\int\limits_1^{\infty}\! \left(1+{1\over r^4}\right)\left(\frac{r}{4}\arctg\dfrac{2r}{r^2 - 1}-\frac{r^2(r^2 - 1)}{2\left(\left(r^2 - 1\right)^2+ 4r^2\right)}\right)dr. \end{align*}$$
Теперь, чтобы избавиться от арктангенса, введем новую переменную $$\psi$$:
$$
\begin{tikzpicture}[domain=1.001:7,scale=0.52725]
\draw[opacity=0] (-0.28,-0.28) rectangle (7.12,3)
\draw[very thin] (-0.1,-0.1) grid (7+0.1,2+0.1);
\draw[->] (-0.2,0)--(7.6,0) node[right] {$r$};
\draw[->] (0,-0.2)--(0,2+0.6) node[right] {$\psi$};
\draw plot (\x,{atan(2*\x/(\x*\x-1))/180*3.14}) node[above right] {$\psi=\arctg\dfrac{2r}{r^2 - 1}$};
\end{tikzpicture}$$
$$\begin{align*}
&\!\!\!r^2-{2\over\tg\psi}r-1=0,\\
r&={1\over\tg\psi}+\sqrt{{1\over\tg^2\psi}+1}={1\over\tg\psi}+{1\over\sin\psi}={\cos\psi+1\over\sin\psi},\\
r^2&={(\cos\psi+1)^2\over1-\cos^2\psi}={\cos\psi+1\over1-\cos\psi},\\
r^2-1&={\cos\psi+1-1+\cos\psi\over1-\cos\psi}={2\cos\psi\over1-\cos\psi},\\
dr&={-\sin^2\psi-\cos\psi(\cos\psi+1)\over\sin^2\psi}d\psi=-{d\psi\over 1-\cos\psi}
.
\end{align*}
$$
Из скетча и выражения для производной видно, что замена монотонная. При решении квадратного уравнения был выбран корень с плюсом, так как мы работаем в области $$r>1$$.
$$\begin{align*}I&=\int\limits_{\pi/2}^{0} \left(1+{(1-\cos\psi)^2\over (\cos\psi+1)^2}\right)\left(\frac{\cos\psi+1}{4\sin\psi}\psi-\frac{\frac{\cos\psi+1}{1-\cos\psi}\frac{2\cos\psi}{1-\cos\psi}}{2\left(\left(\frac{2\cos\psi}{1-\cos\psi}\right)^2+ 4\frac{\cos\psi+1}{1-\cos\psi}\right)}\right){-d\psi\over 1-\cos\psi}=\\ &=\int\limits_{0}^{\pi/2} {2+2\cos^2\psi\over (\cos\psi+1)^2}\left(\frac{\cos\psi+1}{4\sin\psi}\psi-\frac{(\cos\psi+1)\cos\psi}{4\cos^2\psi+ 4({\cos\psi+1})({1-\cos\psi})}\right){d\psi\over 1-\cos\psi}=\\ &=\int\limits_{0}^{\pi/2} {1+\cos^2\psi\over \cos\psi+1}\left(\frac{1}{2\sin\psi}\psi-\frac{\cos\psi}{2\left(\cos^2\psi+ 1-\cos^2\psi\right)}\right){d\psi\over 1-\cos\psi}=\\ &={1\over 2}\int\limits_{0}^{\pi/2} {1+\cos^2\psi\over 1-\cos^2\psi}\left(\frac{\psi}{\sin\psi}-\cos\psi\right)d\psi= {1\over 2}\int\limits_{0}^{\pi/2} {1+\cos^2\psi\over \sin^2\psi}\left(\frac{\psi}{\sin\psi}-\cos\psi\right)d\psi=\\ &={1\over 2}(I_1-I_2)\Bigg|_0^{\pi/2}. \end{align*} $$
Найдем каждый из неопределенных интегралов $$I_1$$ и $$I_2$$ по отдельности. Первый интеграл:
$$\begin{align*} I_1=\int {1+\cos^2\psi\over \sin^2\psi}\frac{\psi}{\sin\psi}\,d\psi= \int {1+\cos^2\psi\over \sin^4\psi}\,\psi\,{\sin\psi}\,d\psi= \int {1+\cos^2\psi\over (1-\cos^2\psi)^2}\,\psi\,d(-\cos\psi). \end{align*} $$
Для интегрирования по частям сначала разложим дробь на простейшие:
$$\begin{align*} {1+x^2\over (1-x^2)^2}&={A\over 1-x}+{B\over (1-x)^2}+{C\over 1+x}+{D\over (1+x)^2}=\\ &={A(1-x)(1+x)^2+B(1+x)^2+C(1+x)(1-x)^2+D(1-x)^2\over (1-x^2)^2}. \end{align*}$$
Если приравнять числители и подставить $$x=1$$, получим $$B=1/2$$. При подстановке $$x=-1$$ получаем $$D=1/2$$. Так как $$B(1+x)^2+D(1-x)^2$$ уже дает $$1+x^2$$, $$A=C=0$$.
$$ \int\!{1+x^2\over (1-x^2)^2}\,dx=\int\!{dx\over 2(1-x)^2}+\int\!{dx\over 2(1+x)^2}={1\over 2(1-x)}-{1\over 2(1+x)}+C={x\over 1-x^2}+C. $$
$$\begin{align*} I_1=-\psi{\cos\psi\over 1-\cos^2\psi} +\int {\cos\psi\over 1-\cos^2\psi}d\psi=-\psi{\cos\psi\over \sin^2\psi}-{1\over\sin\psi}+C. \end{align*} $$
Второй интеграл:
$$\begin{align*} I_2=\int {1+\cos^2\psi\over \sin^2\psi}\cos\psi\ d\psi= \int {2-\sin^2\psi\over \sin^2\psi}\ d(\sin\psi)=-{2\over\sin\psi}-\sin\psi+C. \\ \end{align*} $$
Наконец, получаем численное значение искомого интеграла:
$$\begin{align*}I&={1\over 2}(I_1-I_2)\Bigg|_0^{\pi/2}={1\over 2}\left(-\psi{\cos\psi\over \sin^2\psi}-{1\over\sin\psi}+{2\over\sin\psi}+\sin\psi\right)\Bigg|_0^{\pi/2}=\\ &={1\over 2}\left({\sin\psi-\psi\cos\psi\over \sin^2\psi}+\sin\psi\right)\Bigg|_0^{\pi/2}= 1-{1\over 2}\lim_{\psi\to0}{\sin\psi-\psi\cos\psi\over \sin^2\psi}=\\ &=1-{1\over 2}\lim_{\psi\to0}{\psi+o(\psi^2)-\psi+o(\psi^2)\over \psi^2+o(\psi^2)}=1. \end{align*}$$
Простейшая модель электрона: электромагнитная масса и гиромагнитное отношение
Продолжим развлекаться с классической электродинамикой. В прошлый раз мы подсчитали момент импульса в системе, состоящей из магнитного момента (маленькой катушки) в центре большой равномерно заряженной сферы
$$\vec{L}={2\over 3}{Q\vec{\mathfrak{m}}\over ca}.$$(1)
Но магнитное поле вокруг сферы можно создать без дополнительной катушки, просто закрутив ее. Получается, что часть момента импульса вращающейся сферы запасается в ее электромагнитном поле. Определим эту добавку.
Магнитный момент вращающейся сферы
Мы собираемся показать, что магнитное поле вне равномерно заряженной сферы радиуса a и заряда Q, вращающейся с угловой скоростью ω, точно совпадает с полем магнитного диполя.
Начинаем с векторного потенциала
$$\vec{A}={1\over c}\int\!{\vec{j}\over r}\,dV={Q\over 4\pi ca^2}\int\!{\vec{v}\over r}\,dS={Q\over 4\pi ca^2}\int\!{\vec{\omega}\times a\vec{n}\over r}\,dS,$$
где $$r=|\vec{R}-a\vec{n}|$$ — расстояние от элемента поверхности dS, задаваемого
$$\vec{A}={Q\over 4\pi ca}\,\vec{\omega}\times\int\!{\vec{n}\over \sqrt{R^2 + a^2-2Ra\cos\chi}}\,dS={Q\over 4\pi ca}\,\vec{\omega}\times\vec{I}.$$
Интеграл $$\vec{I}$$ в последнем выражении — это усреднение единичного вектора $$\vec{n}$$ по направлениям с весом 1/r. Исходя из соображений симметрии ясно, что в результате интегрирования мы получим вектор, параллельный вектору $$\vec{R}$$. Подтвердим это вычислением.
В сферических координатах $$\inline \vec{n}=(\sin\theta\cos\varphi, \sin\theta\sin\varphi, \cos\theta)$$. Направим вектор $$\vec{R}=(0,0,R)$$ вдоль оси z. Тогда угол χ между векторами $$\inline \vec{n}$$ и $$\inline \vec{R}$$ совпадает со сферической координатой θ. Z-компонента интеграла
$$I_z=a^2\int\!\cos\theta\,{1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}\,d(\cos\theta)\,d\varphi.$$
Известно, что функцию 1/r можно разложить по многочленам Лежандра (нас интересует область R > a)
$${1\over \sqrt{R^2 + a^2-2Ra\cos\theta}}=\sum\limits_{l=0}^\infty{a^l\over R^{l+1}}P_l(\cos\theta).$$
Подынтегральное выражение состоит из произведения этого ряда на многочлен Лежандра $$P_1(\cos\theta)=\cos\theta$$. Тогда из условия ортогональности
$$\int\limits_{-1}^{1} P_k(x)P_l(x)\,dx={2\over 2k+1}\delta_{kl}$$
сразу следует ответ
$$I_z={4\pi\over 3}{a^3\over R^2}.$$
Компоненты Ix и Iy пропорциональны интегралам от периодических функций sin φ и cos φ, и поэтому равны нулю. Переходя от проекций к вектору, для векторного потенциала получаем
$$\vec{A}={Qa^2\over 3c}\,\vec{\omega}\times{\vec{R}\over R^3}.$$
Таким образом, магнитное поле вне вращающейся сферы совпадает с полем магнитного диполя
$$\vec{\mathfrak{m}}={Qa^2\vec{\omega}\over 3c}.$$(2)
Для полноты отметим, что аналогичными вычислениями легко показать однородность магнитного поля внутри вращающейся сферы.
Электромагнитная масса
Коэффициент в (1) можно переписать
Вслед за Фейнманом мы будем называть электромагнитной массой коэффициент пропорциональности между скоростью равномерного движения сферы и импульсом электромагнитного поля. В нерелятивистском случае
$$\vec{E}=Q{\vec{R}\over R^3},\quad\vec{H}={Q\over c}{\vec{v}\times\vec{R}\over R^3}.$$
Тогда импульс электромагнитного поля дается интегралом
$$\vec{P}={1\over 4\pi c}\int\!\vec{E}\times\vec{H}\,dV={Q^2\over 4\pi c^2}\int\!{1\over R^4}\,\vec{n}\times\left[\vec{v}\times\vec{n}\right]\,dV.$$
Такой интеграл (с точностью до коэффициента) мы вычисляли в прошлый раз, поэтому сейчас просто выпишем ответ
$$\vec{P}={2Q^2 \over 3 ac^2}\,\vec{v}=m_e \vec{v}.$$
Гиромагнитное отношение и модель электрона
Теперь мы можем переписать (1) в таком виде
$$\vec{L}={m_ec\over Q}\,\vec{\mathfrak{m}}.$$
Мы получили интересный результат: гиромагнитное отношение для вращающейся безмассовой заряженной сферы совпадает с гиромагнитным отношением электрона.
Обычно в литературе по квантовой механике утверждается, что нельзя представлять себе спин электрона как его вращение, так как в такой модели скорость точек на его поверхности будет больше скорости света. Сейчас мы в этом убедимся.
Подставим в (1) магнитный момент (2) и спин электрона ½:
$${\hbar\over 2}={2\over 3}\,{Q\over ca}\,{Qa^2\omega\over 3c},$$
откуда отношение экваториальной скорости к скорости света есть
$${a\omega\over c}={9\over 4}\,{\hbar c\over Q^2}={9\over 4\alpha}\approx308.$$
Несостоятельность простейшей модели электрона проявляется и в том, что полная энергия электрического поля
$$U={1\over 8\pi}\int\!{E^2}\,dV={1\over 8\pi}\int\limits_a^{\infty}{Q^2\over R^4}\,4\pi R^2\,dR={Q^2 \over 2a}={4\over 3}\,m_ec^2$$
отличается от ожидаемой величины mec2.