Брахистохрона и свободное падение зарядов в дополнительном магнитном поле

Вернемся к задаче о брахистохроне — кривой скорейшего спуска. Иоганн Бернулли доказал, что в однородном поле тяжести такой кривой является циклоида.

Есть еще одна задача на движение частиц, в которой ответом тоже является циклоида, — задача о падении заряда в однородном магнитном поле. Эта задача эквивалентна движению заряженной частицы в ортогональных однородных электрическом и магнитном поле с нулевой начальной скоростью. Ее можно решать переходом в движущуюся систему отсчета, в которой электрическое поле зануляется и частица движется по окружности в магнитном поле. Комбинация поступательного движения по прямой и вращательного движения по окружности и дает циклоиду.

$$ \begin{tikzpicture}[scale=0.5] \draw[->] (-0.5,0) -- (20.5,0) node[right] {\( x \)}; \draw[->] (0,0.5) -- (0,-4) node[below] {\( y \)}; \foreach \x in {1,3.1,...,20} { \foreach \y in {0.5,-0.9,...,-4} { \draw[thick,blue] (\x,\y) node {\small\(\otimes\)}; } } \node[blue] at (-1,-3.5) {\(\vec{B}\)}; \draw[->,thick,red] (-1,0.5) -- +(0,-2) node[below] {\( \vec{E} \)}; \draw[thick,smooth,samples=100,domain=0:18.7] plot({\x-sin(deg(\x))},{cos(deg(\x))-1}); \foreach \x in {2,8.29,...,20} \draw[->,thick] ({\x-sin(deg(\x))}, {cos(deg(\x))-1}) -- ++(0.2, -0.1); \end{tikzpicture} $$

В прошлый раз мы занимались брахистохроной в центрально-симметричном силовом поле с потенциалом $$r^2$$ и обсудили, что ответом является дуга гипоциклоиды. Можно задать аналогичный вопрос и о свободном движении заряженной частицы: какова траектория заряда в потенциале $$r^2$$ и однородном магнитном поле, перпендикулярном плоскости движения заряда?

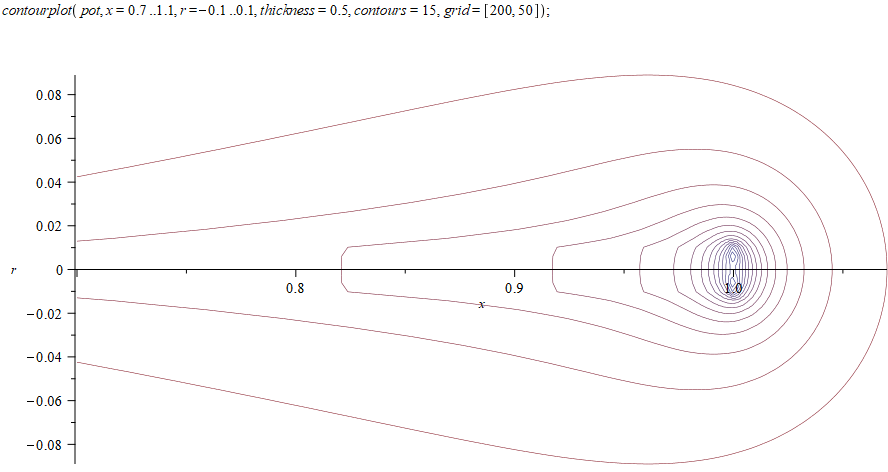
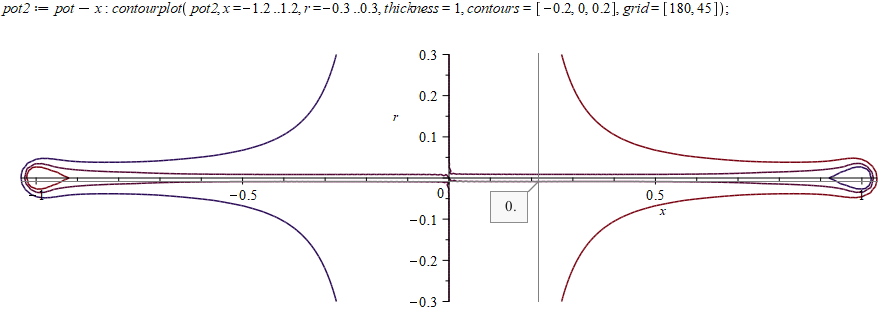
Из качественных соображений понятно, что траектория будет «звездообразной». Во-первых, заряд действительно всегда движется в одной плоскости, так как нет сил, не лежащих в этой плоскости. Во-вторых, когда заряд отпускают, он начинает двигаться к центру притяжения. По мере роста скорости увеличивается и магнитная сила, направленная перпендикулярно траектории и отклоняющая заряд в сторону. Заряд разворачивается, тормозится и останавливается на том же расстоянии от центра, на котором он был в начальном положении. Дальше этот цикл повторяется.

Численное решение уравнений движения показывает траекторию, очень напоминающую гипоциклоиду. Давайте разберемся, действительно ли заряд в магнитном поле и потенциале $$r^2$$ будет двигаться по гипоциклоиде и случайно ли траектория опять совпадает с брахистохроной?

Падение в «вертикальном» поле

Направим ось y вниз и будем рассматривать движение в поле с потенциальной энергией $$U(x,y,z)=-mf(y)$$, причем $$f(0)=0$$. Из закона сохранения энергии $$v^2=2f(y)$$. Брахистохрона минимизирует интеграл для времени движения:

$$t=\int {dl\over v}=\int {\sqrt{dx^2+dy^2\over 2f(y)}}={1\over\sqrt{2}}\int {\sqrt{y'^2+1\over f(y)}}\ dx.$$

Первый интеграл соответствующего уравнения Эйлера — Лагранжа имеет вид

$$\frac{1}{K_1^2} = (y'^2 + 1) f(y).$$(1)

Это дифференциальное уравнение для линейного потенциала $$f(y)=gy$$, то есть для однородного силового поля, описывает циклоиду.

Рассмотрим теперь свободное движение заряда в том же потенциале и горизонтальном магнитном поле (в этой системе координат оно направлено вдоль оси z). Выберем векторный потенциал в виде $$\vec{A}=(-yB,0,0)$$. Лагранжиан заряженной частицы в однородном магнитном поле

$${\cal L}={mv^2\over 2}-U+q\vec{v}\cdot\vec{A}=\frac{m}{2}\left(\dot{x}^2+\dot{y}^2\right)+mf(y)-qB\dot{x}.$$

Лагранжиан не зависит явно от времени и координаты x, поэтому энергия и обобщенный импульс сохраняются:

$$p_x = m \dot{x} - q B y,\quad E = \dfrac{m}{2}\left( \dot{x}^2 + \dot{y}^2 \right) - mf(y).$$

В начальном положении энергия и импульс равны нулю, поэтому:

$$\begin{cases} 0=m\dot{x}-qBy,\\ 0=\cfrac{1}{2}\left(\dot{x}^2 + \dot{y}^2\right)-f(y). \end{cases} \Leftrightarrow \begin{cases} \dot{x}&=\dfrac{qB}{m}y,\\ f(y)\!\!\!\!&=\cfrac{1}{2}\left(\dot{x}^2 + \dot{y}^2\right). \end{cases}$$

$$f(y)={1\over2}\dot{x}^2(y'^2+1)={q^2B^2\over 2m^2}y^2(y'^2+1).$$(2)

Полученное дифференциальное уравнение (2) траектории заряда в поле притяжения и магнитном поле совпадает с уравнением брахистохроны (1) только если $$f(y)\sim y$$. Таким образом, свободное движение в силовом и магнитном полях имеет ту же траекторию, что и брахистохрона в силовом поле, только если это однородное поле.

Падение в центральном поле

В прошлый раз мы находили уравнение брахистохроны в поле с потенциалом $$g(r)\sim r^2$$. Если проделать те же выкладки для произвольного потенциала, получим следующее дифференциальное уравнение:

$$k^2\left(r'^2+r^2\right)\left(g(r_0)-g(r)\right)=r^4.$$(3)

Перейдем теперь к свободному движению заряда в этом поле и дополнительном магнитном поле.

$$\usetikzlibrary{calc} \begin{tikzpicture}[scale=1.25] \foreach \x in {-2.3,-0.8,...,3} { \foreach \y in {-2.3,-0.8,...,3} { \draw[thick,blue] (\x,\y) node {\small\(\odot{}\)}; } } \draw[->] (0,0) -- (2.5,0) node[right] {$x$}; \draw[] (0,0) circle (2); \def\a{0.3} \def\b{2} \newcommand{\xt}[1]{(\b-\a)*cos(#1)+\a*cos((\b-\a)*#1/\a} \newcommand{\yt}[1]{(\b-\a)*sin(#1)-\a*sin((\b-\a)*#1/\a} \draw[thick,domain=0:110,smooth,variable=\t,samples=100] plot ({\xt{\t}},{\yt{\t}}); \def\t{25} \def\q{25.1} \coordinate (P) at ({\xt{\t}},{\yt{\t}}); \coordinate (P1) at ({\xt{\q}},{\yt{\q}}); \draw[->] (0,0) -- (P) node[midway,above] {$r$}; \draw[->] ($(P)!0!(P1)$) -- ($(P)!130!(P1)$) node[left] {$\vec{v}$}; \draw[->] (0.95,0) arc (0:22:0.95); \node at (1.1,0.2) {$\theta$}; \end{tikzpicture}$$

В силу наличия вращательной симметрии удобно выбрать векторный потенциал в форме $$\vec{A}=\vec{B}\times\vec{r}/2$$. Лагранжиан заряженной частицы

$${\cal L}={mv^2\over 2}-U+q\vec{v}\cdot\vec{A}= \frac{m}{2}\left(\dot{r}^2+r^2\dot{\varphi}^2\right)-mg(r)+{qB\over2}r^2\dot{\varphi}.$$

Первые интегралы для уравнения Эйлера — Лагранжа дают сохранение энергии и обобщенного момента импульса:

$$\begin{cases} \dfrac{2E}{m}\!\!\!\!&=r^2\dot{\varphi}^2+\dot{r}^2+2g(r),\\ L&=r^2(m\dot{\varphi}+\dfrac{1}{2}qB). \end{cases}$$

Так как в начальный момент $$r(0)=r_0$$, а скорость равна нулю, то:

$$\begin{cases} 2g(r_0)\!\!\!\!&=r^2\dot{\varphi}^2+\dot{r}^2+2g(r),\\ r_0^2\dfrac{1}{2}qB\!\!\!\!&=r^2(m\dot{\varphi}+\dfrac{1}{2}qB). \end{cases} \Leftrightarrow \begin{cases} 2g(r_0)-2g(r)\!\!\!\!&=\dot{\varphi}^2(r^2+r'^2),\\ \dot{\varphi}r^2&=(r_0^2-r^2)\dfrac{qB }{2m}. \end{cases}$$

$$2(g(r_0)-g(r))=(r^2+r'^2)\left({r_0^2\over r^2}-1\right)^2\dfrac{q^2B^2}{4m^2}.$$(4)

Перемножив (3) на (4), получаем

$$2k^2\left(g(r_0)-g(r)\right)^2=\left(r_0^2 - r^2\right)^2\dfrac{q^2B^2}{4m^2}.$$

Мы видим, что только при $$g(r)\sim r^2$$ уравнения (3) и (4) совместимы.

Совпадение брахистохроны и траектории падения заряженной частицы в дополнительном магнитном поле оказалось случайным. Оно имеет место только для однородного поля притяжения и для осцилляторного потенциала в центрально-симметричном случае. Для других потенциалов дифференциальные уравнения различаются, поэтому совпадения не будет.

Задача о математическом ожидании количества случайных слагаемых

Недавно Майкл Пенн разбирал интересную задачу, которую я cформулирую так:

Сколько в среднем нужно взять случайных натуральных чисел, равномерно распределенных на отрезке от 1 до $$n$$, чтобы их сумма превысила $$n$$?

Конструкция в его решении выглядит достаточно искусственной и требует непростых рассуждений. Я предлагаю решить задачу «в лоб», без применения хитрых конструкций. Оказывается, это можно сделать, немного повозившись с преобразованием сумм.

Решение

Ясно, что одного числа $$a_1\in[1,n]$$ недостаточно, чтобы сумма $$a_1$$ превысила $$n$$. Два числа уже могут в сумме $$a_1+a_2$$ дать число, большее $$n$$. Если это произошло, испытание завершается. В противоположном случае нужно выбрать еще одно число и т. д.

Обозначим через $$P_n(k)$$ вероятность неуспеха — вероятность того, что сумма случайно выбранных $$k$$ чисел окажется не больше $$n$$:

$$P_n(k)=P\left(\sum\limits_{i=1}^{k}a_i\leq n\right).$$(1)

Cхему одного испытания можно представить в виде дерева, где добавление нового числа при неуспехе каждый раз порождает развилку:

$$ \tikzstyle{level 1}=[level distance=5cm] \tikzstyle{level 2}=[level distance=6cm] \tikzstyle{bag}=[fill=red!20] \tikzstyle{end}=[fill=green!20] \begin{tikzpicture}[grow=right, sloped,sibling distance = 15mm] \node[bag, label=above:{$P_n(1)=1$}] {$a_1\leq n$} child[edge from parent/.style={draw, -latex, line width=0.8mm, black!30}] { node[end] {$a_1+a_2>n$} edge from parent node[below,black] {$P_n(1)-P_n(2)$} } child[edge from parent/.style={draw, -latex, line width=3mm, black!30}] { node[bag] {$a_1+a_2\leq n$} child[edge from parent/.style={draw, -latex, line width=1.2mm, black!30}] { node[end] {$a_1+a_2+a_3>n$} edge from parent node[below,black] {$P_n(2)-P_n(3)$} } child[edge from parent/.style={draw, -latex, line width=1.8mm, black!30}] { node[bag, label=right:{...}] {$a_1+a_2+a_3\leq n$} edge from parent node[above,black] {$P_n(3)$} } edge from parent node[above,black] {$P_n(2)$} }; \end{tikzpicture} $$

Из нее мы видим, что вероятность того, что в одном испытании будет взято ровно $$k$$ чисел, равна $$P_n(k-1)-P_n(k)$$. Действительно, событие, противоположное (1), состоит в том, что сумма произвольного не превосходящего $$k$$ количества случайно взятых чисел будет больше $$n$$. Его вероятность есть $$1-P_n(k)$$. Аналогично, вероятность того, что сумма произвольного не превосходящего $$k-1$$ количества случайно взятых чисел будет больше $$n$$ есть $$1-P_n(k-1)$$. Разность этих величин как раз и дает $$P_n(k-1)-P_n(k)$$.

Тогда искомое среднее $$N$$ можно выразить как

$$\begin{align*}N&=2\left[P_n(1)-P_n(2)\right]+3\left[P_n(2)-P_n(3)\right]+\ldots+(n+1)\left[P_n(n)-P_n(n+1)\right]=\\ &=2+P_n(2)+P_n(3)+P_n(4)+\ldots+P_n(n).\end{align*}$$(2)

В этой сумме мы раскрыли скобки и сгруппировали промежуточные слагаемые. Ясно, что дерево вероятностей конечно, и последняя ненулевая вероятность $$P_n(n)=1/n^n$$ в нем соответствует случаю $$a_1=a_2=\ldots=a_n=1$$. Поэтому сумма в (2) заканчивается на нулевом слагаемом $$-(n+1)P_n(n+1)=0$$, тем самым кроме сгруппированных промежуточных слагаемых никаких слагаемых в конце в ней нет.

Начнем с вычисления $$P_n(2)$$. Пространство элементарных событий для двух натуральных чисел от 1 до $$n$$ можно представить матрицей $$n\times n$$, в которой неудачные исходы $$a_1+a_2\leq n$$ расположены под главной диагональю:

$$ \tikzstyle{bad}=[fill=red!10!white, minimum width=0.98cm, minimum height=0.98cm] \tikzstyle{good}=[fill=green!10!white, minimum width=0.98cm, minimum height=0.98cm] \begin{tikzpicture}[scale=1] \draw[step=1] (0,0) grid (5,5); \node[bad] at (0.5,0.5) {2}; \node[bad] at (1.5,0.5) {3}; \node[bad] at (0.5,1.5) {3}; \node[good] at (4.5,4.5) {$2n$}; \foreach \x in {0,...,4} { \node[good] at (0.5+\x, 4.5-\x) {$n$+1}; } \foreach \x in {0,...,3} { \node[good] at (1.5+\x, 4.5-\x) {$n$+2}; } \foreach \x in {0,...,2} { \node[good] at (2.5+\x, 4.5-\x) {}; } \foreach \x in {0,...,1} { \node[good] at (3.5+\x, 4.5-\x) {}; } \foreach \x in {0,...,3} { \node[bad] at (0.5+\x, 3.5-\x) {$n$}; } \foreach \x in {0,...,2} { \node[bad] at (0.5+\x, 2.5-\x) {}; } \draw[->] (0,-0.5) -- ++(5,0) node[pos=0.5,below] {$a_1$}; \draw[->] (-0.5,0) -- ++(0,5) node[pos=0.5,left] {$a_2$}; \end{tikzpicture} $$

Искомая вероятность $$P_n(2)$$ равна отношению количества красных квадратиков к общему количеству квадратиков. Вычисляя, получаем, что она связана с треугольными числами $$T_n=n(n+1)/2$$:

$$P_n(2)={1\over n^2}\sum\limits_{a_1+a_2\leq n}1={1\over n^2}\sum\limits_{a_1=1}^{n-1}\left(n-a_1\right)={1\over n^2}\cdot{(n-1)n\over 2}={T_{n-1}\over n^2}={C_n^2\over n^2}.$$

Перейдем к $$P_n(3)$$. Пространство элементарных событий для трех чисел можно представить себе как часть куба $$n\times n\times n$$, нарезанного на единичные кубики. Нас интересуют неудачные исходы $$a_1+a_2+a_3\leq n$$, которые соответствуют такой пирамидке:

$$ \usetikzlibrary {perspective} \colorlet{cube color}{blue!50!cyan} \begin{tikzpicture}[3d view={110}{25},scale=0.8, line join=round, line cap=round,every path/.style={cube color,thick}] \def\k{1.2} \def\n{2} \draw[black,thin,->] (0,0) -- ++(0,4.4) node[pos=0.9,above] {$a_1$}; \draw[black,thin,->] (0,0) -- ++(4.5,0) node[pos=0.9,left] {$a_2$}; \draw[black,thin,->] (0,0,0) -- ++(0,0,4.2) node[pos=0.9,left] {$a_3$}; \foreach \z in {0,...,\n} { \pgfmathsetmacro{\ymax}{\n-\z} \foreach \y in {0,...,\ymax} { \pgfmathsetmacro{\xmax}{\ymax-\y} \foreach \x in {0,...,\xmax} { \draw[fill=cube color!30] (\k*\x, \k*\y, \k*\z+1) -- ++(1, 0, 0) -- ++(0, 1, 0) -- ++(-1, 0, 0) -- cycle; \draw[fill=cube color!50] (1+\k*\x, \k*\y, \k*\z) -- ++(0, 0, 1) -- ++(0, 1, 0) -- ++(0, 0, -1) -- cycle; \draw[fill=cube color!70] (\k*\x, \k*\y+1, \k*\z) -- ++(1, 0, 0) -- ++(0, 0, 1) -- ++(-1, 0, 0) -- cycle; } } } \end{tikzpicture}$$

Здесь мы можем предположить, что вероятность $$P_n(3)$$ выражается через тетраэдральные числа $$\inlineTe_n=\sum_{k=1}^nT_n$$. Формально этот результат получается при вычислении суммы на множестве $$a_1+a_2+a_3\leq n$$ по слоям: сначала по слою $$a_1+a_2+a_3=n$$, потом по слою $$a_1+a_2+a_3=n-1$$ и т. д:

$$ \usetikzlibrary {perspective} \colorlet{cube color}{blue!50!cyan} \begin{tikzpicture}[3d view={110}{25},scale=0.8, line join=round, line cap=round,every path/.style={cube color,thick}] \def\k{1.2} \def\n{2} \foreach \z in {0,...,\n} { \pgfmathsetmacro{\ymax}{\n-\z} \foreach \y in {0,...,\ymax} { \pgfmathsetmacro{\xmax}{\ymax-\y} \foreach \x in {0,...,\xmax} { \pgfmathtruncatemacro{\layer}{\x + \y + \z} \ifnum \layer=2 \colorlet{cube color}{blue!50!cyan} \fi \ifnum \layer=1 \colorlet{cube color}{olive} \fi \ifnum \layer=0 \colorlet{cube color}{orange} \fi \draw[fill=cube color!30] (\k*\x, \k*\y, \k*\z+1) -- ++(1, 0, 0) -- ++(0, 1, 0) -- ++(-1, 0, 0) -- cycle; \draw[fill=cube color!50] (1+\k*\x, \k*\y, \k*\z) -- ++(0, 0, 1) -- ++(0, 1, 0) -- ++(0, 0, -1) -- cycle; \draw[fill=cube color!70] (\k*\x, \k*\y+1, \k*\z) -- ++(1, 0, 0) -- ++(0, 0, 1) -- ++(-1, 0, 0) -- cycle; \pgfmathsetmacro{\s}{5.5+5*(\n-\layer)} \pgfmathsetmacro{\p}{-1-2.5*(\n-\layer)} \pgfmathsetmacro{\t}{0.45} \draw[fill=cube color!30] (\k*\x+\p, \k*\y+\s, \k*\z+1+\t) -- ++(1, 0, 0) -- ++(0, 1, 0) -- ++(-1, 0, 0) -- cycle; \draw[fill=cube color!50] (1+\k*\x+\p, \k*\y+\s, \k*\z+\t) -- ++(0, 0, 1) -- ++(0, 1, 0) -- ++(0, 0, -1) -- cycle; \draw[fill=cube color!70] (\k*\x+\p, \k*\y+1+\s, \k*\z+\t) -- ++(1, 0, 0) -- ++(0, 0, 1) -- ++(-1, 0, 0) -- cycle; } } } \node[black] at (0,4,1.25) {$=$}; \node[black] at (0,10,2.25) {$+$}; \node[black] at (0,15.5,3.15) {$+$}; \end{tikzpicture}$$

$$\begin{align*} P_n(3)&={1\over n^3}\sum\limits_{a_1+a_2+a_3\leq n}1={1\over n^3}\left(\sum\limits_{a_1+a_2+a_3=n}1+\sum\limits_{a_1+a_2+a_3=n-1}1+\ldots\right)=\\ &={1\over n^3}\left(\sum\limits_{a_1+a_2\leq n-1}1+\sum\limits_{a_1+a_2\leq n-2}1+\ldots\right). \end{align*}$$

Каждая из сумм в скобках уже вычислена на предыдущем этапе. Действительно, количество элементов в слоях задается треугольными числами. Подставляем:

$$P_n(3)={1\over n^3}(T_{n-2}+T_{n-3}+\ldots)={Te_{n-2}\over n^3}={C_n^3\over n^3}.$$

Идея с послойным вычислением суммы без каких-либо изменений обобщается на случай произвольного количества чисел $$k$$. Вероятность $$P_n(k)$$ будет выражаться через гипертетраэдральные числа:

$$P_n(k)={C_n^k\over n^k}.$$(3)

Подставим в (2):

$$N=2+{C_n^2\over n^2}+{C_n^3\over n^3}+{C_n^4\over n^4}+\ldots+{C_n^n\over n^n}.$$

А это есть не что иное, как разложение $$(1+1/n)^n$$ через бином Ньютона. Ответ:

$$N=\left(1+{1\over n}\right)^n.$$

Обсуждение

В пределе неограниченно больших $$n$$ ожидаемое количество слагаемых стремится к $$e$$. Да и сама задача в этом пределе переходит в известную задачу о математическом ожидании количества случайных величин, равномерно распределенных на интервале от 0 до 1, таких чтобы их сумма превзошла 1. О том, что это математическое ожидание равно $$e$$, я узнал из книги Мартина Гарднера «Математические досуги»:

Идея рассуждений в непрерывном случае аналогична нашему решению, а детали вычислений оказываются проще. Суммы заменяются на интегралы от многочленов, которые без проблем вычисляются и дают меру симплекса, построенного на единичных отрезках на осях координат: $$P(k)=1/k!$$. Сумма в (2) становится бесконечной и превращается в известный ряд для числа $$e=1+1/1!+1/2!+\ldots$$

В дискретном случае приходится заниматься конечными суммами, которые сводятся к треугольным числам и их обобщениям. Надо сказать, что для решения никакие их свойства не использовались. Явный вид $$P_n(k)$$ можно было получить для нескольких начальных $$k$$ и затем по индукции доказать общий вид (3). Либо можно воспользоваться свойствами чисел, стоящих на местах с номером $$k$$ в треугольнике Паскаля:

$$ \makeatletter \newcommand\binomialcoefficient[2]{ % Store values \c@pgf@counta=#1% n \c@pgf@countb=#2% k % % Take advantage of symmetry if k > n - k \c@pgf@countc=\c@pgf@counta% \advance\c@pgf@countc by-\c@pgf@countb% \ifnum\c@pgf@countb>\c@pgf@countc% \c@pgf@countb=\c@pgf@countc% \fi% % % Recursively compute the coefficients \c@pgf@countc=1% will hold the result \c@pgf@countd=0% counter \pgfmathloop% c -> c*(n-i)/(i+1) for i=0,...,k-1 \ifnum\c@pgf@countd<\c@pgf@countb% \multiply\c@pgf@countc by\c@pgf@counta% \advance\c@pgf@counta by-1% \advance\c@pgf@countd by1% \divide\c@pgf@countc by\c@pgf@countd% \repeatpgfmathloop% \the\c@pgf@countc% } \makeatother \begin{tikzpicture}[scale=0.8] \node[red, right] at (0.7,-0.5) {$_\swarrow\ \text{Натуральные числа}$}; \node[orange, right] at (1.2,-1.5) {$_\swarrow\ \text{Треугольные числа}$}; \node[olive, right] at (1.7,-2.5) {$_\swarrow\ \text{Тетраэдральные числа}$}; \node[right] at (2.4,-3.5) {...}; \foreach \n in {0,...,7} { \foreach \k in {0,...,\n} { \ifnum \k=0 \node[black] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=1 \node[red,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=2 \node[orange,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=3 \node[olive,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=4 \node[green!70!black,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=5 \node[blue,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=6 \node[magenta,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi \ifnum \k=7 \node[purple,node font=\bf] (\n\k) at (\k-\n/2,-\n) {\binomialcoefficient{\n}{\k}}; \fi } } \end{tikzpicture}$$

Задача коллекционера

Представьте, что вы кидаете игральный кубик, и выпадает число от 1 до 6. Сколько раз в среднем нужно бросить кубик до того момента, как каждое число выпадет хотя бы один раз? Ясно, что число попыток не должно быть меньше 6. Но если при этом попадались одинаковые числа, потребуется больше бросков. Сколько именно?

Это одна из возможных формулировок задачи коллекционера. Под таким названием (Coupon Collector’s Problem) она встречается в англоязычной литературе, а в русскоязычной практически не упоминается (я нашел одну публикацию в «Математическом просвещении»). Давайте исправим несправедливость и разберем эту весьма интересную задачу.

Современному читателю проще прочувствовать смысл этой задачи на примере киндер-сюрприза: сколько нужно купить шоколадных яиц, внутри которых находится одна из $$N$$ машинок, чтобы собрать полную коллекцию?

Стандартное решение

Обозначим через $$T$$ искомое количество попыток сбора $$N$$ элементов коллекции. Оно состоит из суммы числа попыток $$t_i$$ получить элемент $$i$$, когда уже собрано $$i-1$$ элементов: $$T=t_1 + \cdots + t_N$$.

Вероятность найти новый $$i$$-й элемент коллекции, когда уже собрано $$i-1$$ элементов и осталось собрать $$N-i+1$$, равна

$$P(i)={N-i+1\over N}.$$(1)

То есть $$t_i$$ — случайная величина с геометрическим распределением и математическим ожиданием

$$\operatorname{E}(t_i)=\frac{1}{P(i)}=\frac{N}{N-i+1}.$$(2)

С учетом линейности математического ожидания

$$\begin{align*} \operatorname{E}(T) & {}= \operatorname{E}(t_1 + t_2 + \cdots + t_N)=\\ &=\operatorname{E}(t_1) + \operatorname{E}(t_2) + \cdots + \operatorname{E}(t_N)=\\ &=\frac{1}{P(1)} + \frac{1}{P(2)} + \cdots + \frac{1}{P(N)}=\\ &=\frac{N}{N} + \frac{N}{N-1} + \cdots + \frac{N}{1}=\\ &=N \cdot \left(\frac{1}{1} + \frac{1}{2} + \cdots + \frac{1}{N}\right)=\\ &=N H_N. \end{align*}$$

Здесь $$H_N$$ — частичные суммы гармонического ряда, асимптотика которых выражается через логарифм:

$$\operatorname{E}(T)=NH_{N}=N\ln N+\gamma N+{1\over 2}+O\left({1\over N}\right).$$(3)

Альтернативное решение

Решение выше получилось достаточно простым благодаря тому, что вероятность получения нового элемента коллекции (1) не зависит от истории, то есть от самих величин $$t_i$$. Однако такая зависимость может появиться в более сложном случае. Скажем, если коллекционер обменивается с другими коллекционерами, то чем больше у него накопилось дублей в коллекции, тем больше вероятность получить новый элемент через обмен. В этом примере формула (1) усложняется, а (2) вообще не работает.

В общем случае вероятность появления нового элемента может явно зависеть от номера шага $$t$$. Через $$P_t(n)$$ мы обозначим вероятность того, что после $$t$$ шагов мы собрали $$n$$ элементов коллекции. Я проведу рассуждения в условиях исходной задачи, а вы при необходимости можете их обобщить.

Если после выполнения $$t$$ шагов мы собрали $$n$$ элементов, это значит, что на предыдущем шаге количество элементов могло быть либо $$n-1$$, либо $$n$$. В первом случае мы получаем новый элемент с вероятностью, определяемой формулой (1), во втором случае противоположной вероятностью:

$$P_t(n)=\left(1-{n-1\over N}\right)P_{t-1}(n-1)+{n\over N}P_{t-1}(n).$$(4)

Это уравнение вместе с граничными условиями содержит в себе всю информацию из условия задачи, поэтому все остальные рассуждения будут чисто техническими.

О каких граничных условиях идет речь? Ясно, что $$P_0(0)=1$$, $$P_0(n)=0, 0<n\leq N$$ (в начале никакой коллекции нет). Кроме того, на первом шаге мы гарантированно получим один элемент, поэтому $$P_t(0)=0, t>0$$.

Перепишем для удобства (4) в другом виде после подстановки $$n=N-m$$:

$$P_t(N-m)={m+1\over N}P_{t-1}\left(N-(m+1)\right)+{N-m\over N}P_{t-1}(N-m)$$(4a)

Заметим еще, что на каждом шаге должна сохраняться нормировка вероятности — в коллекции точно должно быть хоть сколько-то элементов:

$$\sum_{n=0}^N P_t(n)=1.$$(5)

Нарушение условия нормировки сразу укажет на ошибку в построении математической модели. Давайте проверим, что в (4) подобных ошибок нет:

$$\begin{align*} \sum_{n=0}^N P_t(n)&=P_t(0)+\sum_{n=1}^N \left[\left(1-{n-1\over N}\right)P_{t-1}(n-1)+{n\over N}P_{t-1}(n)\right]=\\ &=\sum_{n=0}^{N-1} \left(1-{n\over N}\right)P_{t-1}(n)+\sum_{n=1}^N {n\over N}P_{t-1}(n)=\\ &=\sum_{n=0}^{N-1}P_{t-1}(n)-{0\over N}P_{t-1}(0)+{N\over N}P_{t-1}(N)=\\ &=\sum_{n=0}^{N}P_{t-1}(n). \end{align*}$$

Мы опустили нулевое слагаемое $$P_t(0)$$ из граничных условий, а также перенумеровали слагаемые в одной из сумм. По индукции видно, что нормировка сохраняется на каждом шаге.

В задаче нам нужно усреднить число попыток $$t$$ до окончания сбора коллекции:

$$\operatorname{E}(T)=\sum\limits_tt\left(P_t(N)-P_{t-1}(N)\right).$$

Чтобы получить вероятность окончания сбора коллекции именно на шаге $$t$$, я вычел из вероятности собрать $$N$$ элементов на шаге $$t$$ вероятность собрать $$N$$ элементов на шаге $$t-1$$ (вычитается вероятность того, что на предыдущем шаге коллекция уже собрана).

Из (4а) при $$m=0$$:

$$P_t(N)={1\over N}P_{t-1}\left(N-1\right)+P_{t-1}(N).$$

Отсюда

$$\operatorname{E}(T)={1\over N}\sum\limits_ttP_{t-1}(N-1).$$(6)

Здесь мы видим другое представление вероятности окончания сбора коллекции: вероятность сбора последнего элемента $$1/N$$ умножается на вероятность наличия $$N-1$$ элементов на предыдущем шаге.

Идея дальнейших вычислений в том, чтобы пользуясь равенством (4а) и дальше понижать аргумент в (6) от $$N-1$$ до 0. Тогда в сумме останется только один ненулевой элемент, соответствующий $$P_0(0)=1$$. Вы можете проделать несколько подстановок (4а) вручную и увидеть закономерность. Я же сразу сформулирую ее в виде утверждения, связывающего $$\operatorname{E}(T)$$ и $$P_{t}(N-m)$$:

Утверждение. Существуют такие числа $$A_m$$ и $$B_m$$, что при любых натуральных $$N$$ и $$m\in [1,N]$$ выполняется равенство

$$\operatorname{E}(T)={m\over N}\sum\limits_ttP_{t-m}(N-m)+A_mN-B_m.$$(7)

Доказательство по индукции. Если $$m=1$$, то из (6) гипотеза верна при $$A_1=B_1=0$$. Пусть она верна для $$m>1$$. Тогда из (4а)

$$\begin{align*}\operatorname{E}(T)&={m\over N}\sum_tt\left[{m+1\over N}P_{t-m-1}\left(N-(m+1)\right)+{N-m\over N}P_{t-m-1}(N-m)\right]+A_mN-B_m=\\ &={m\over N}{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+{N-m\over N}\underbrace{{m\over N}\sum_ttP_{t-m-1}(N-m)}_{S_1}+A_mN-B_m.\end{align*}$$

Сумма в первом слагаемом похожа на нужную сумму из (7) для $$m$$, увеличенного на 1. Пока отдельно вычислим оставшуюся сумму:

$$\begin{align*}S_1&={m\over N}\sum\limits_ttP_{t-m-1}(N-m)=\\ &={m\over N}\sum_{t+1}(t+1)P_{t-m}(N-m)=\\ &={m\over N}\sum_ttP_{t-m}(N-m)+{m\over N}\sum_tP_{t-m}(N-m)=\\ &=\operatorname{E}(T)-A_mN+B_m+\underbrace{{m\over N}\sum_tP_t(N-m)}_{S_2}.\end{align*}$$

Здесь мы дважды воспользовались изменением индекса суммирования. Так как суммирование идет по всем возможным $$t$$, мы можем спокойно менять индексы. Лишних или отсутствующих слагаемых не будет, так как вероятности зануляются, когда число шагов меньше размера коллекции: $$P_t(n)=0, t<n$$.

Просуммируем теперь (4a) по всем $$t$$:

$$\begin{align*}\sum_tP_t(N-m)&=\sum_t{m+1\over N}P_{t-1}\left(N-(m+1)\right)+\sum_t{N-m\over N}P_{t-1}(N-m)=\\ &={m+1\over N}\sum_tP_t\left(N-(m+1)\right)+{N-m\over N}\sum_tP_t(N-m), \end{align*}$$

откуда

$${m\over N}\sum_tP_t(N-m)=\sum_t{m+1\over N}P_t\left(N-(m+1)\right).$$

Таким образом, по индукции $$\inlineS_2={m\over N}\sum_tP_t(N-m)$$ не зависит от $$m$$ и равно 1, так как при $$m=N$$ переходит в $$P_0(0)+P_1(0)+P_2(0)+\ldots=1+0+0+\ldots=1$$. Возвращаемся к $$\operatorname{E}(T)$$:

$$\begin{align*}\operatorname{E}(T)&={m\over N}{m+1\over N}\sum\limits_ttP_{t-m-1}\left(N-(m+1)\right)+\\ &+{N-m\over N}(\operatorname{E}(T)-A_mN+B_m+1)+A_mN-B_m,\\ N\operatorname{E}(T)&=m{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+\\&+\operatorname{E}(T)N-A_mN^2+B_mN+N-m\operatorname{E}(T)+mA_mN-mB_m-m+A_mN^2-B_mN,\\ m\operatorname{E}(T)&=m{m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+N+mA_mN-mB_m-m,\\ \operatorname{E}(T)&={m+1\over N}\sum_ttP_{t-m-1}\left(N-(m+1)\right)+(A_m+{1/m})N-(B_m+1).\end{align*}$$

По форме это совпадает с (7) при условии

$$A_{m+1}=A_m+{1\over m},\quad B_{m+1}=B_m+1.$$

С учетом начальных условий $$A_1=B_1=0$$ получаем явные выражения коэффициентов: $$A_m=1+1/2+\ldots+1/(m-1)=H_{m-1}$$ — частичные суммы гармонического ряда, $$B_m=m-1$$. $$\square$$

Подставим теперь $$m=N$$ в (7). Тогда

$$\omeratorname{E}(T)=\sum_ttP_{t-N}(0)+H_{N-1}N-N+1=H_{N-1}N+1=N\left(H_{N-1}+{1\over N}\right)=NH_N,$$

что совпадает с ответом стандартного решения.

Вывод

Мы решили задачу коллекционера, записав уравнение эволюции распределения вероятности (4). Это уравнение можно рассматривать как дискретный вариант уравнения, описывающего поток вероятности.

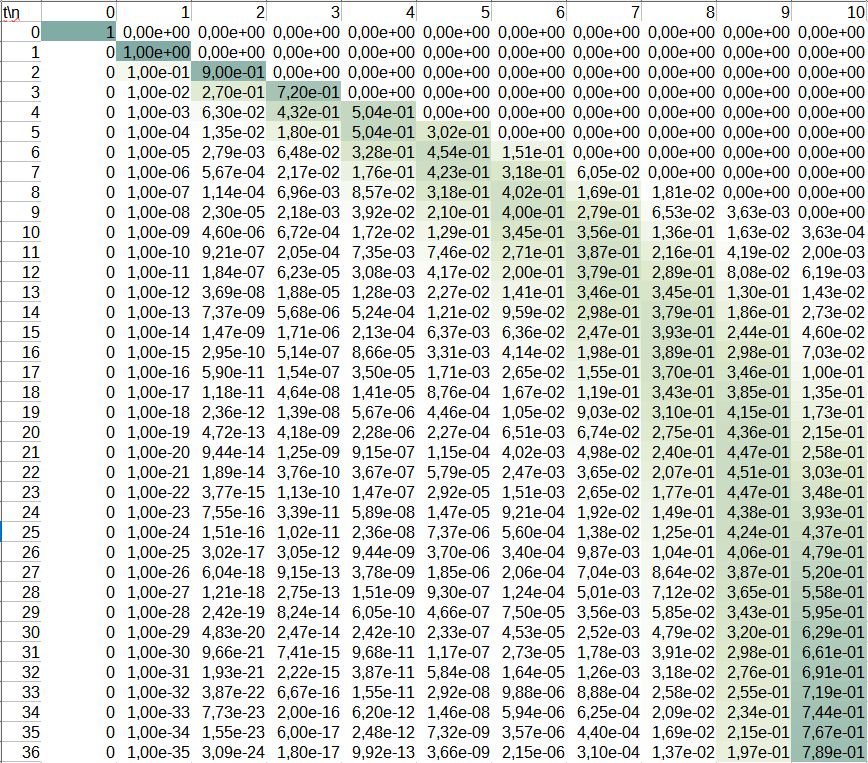
Такой подход универсален для задач подобного типа, потому что позволяет их решать не только аналитически, но и численно. Например, в нашем случае эволюцию распределения вероятности можно рассчитать на основе уравнения (4) даже в Excel. На скриншоте видно, как распределение вероятности со временем смещается от меньших $$n$$ к большим для $$N=10$$.

Как создается электрическое поле в проводнике с током?

Мотивация

Вопрос, вынесенный в заголовок, в свое время породил большую дискуссию на физическом форуме (1, 2, 3). Вот более точная формулировка вопроса:

Рассмотрим длинный провод, подключенный к батарейке. По нему течет постоянный ток. Ток создается электрическим полем Е, которое, в свою очередь, создается зарядами на полюсах батарейки. Почему вдали от полюсов (например, в середине проводника) поле Е=const, а не убывает при удалении от полюсов, как ему положено по закону Кулона?

Правильный ответ заключается в том, что батарейка не является единственным источником электрического поля, какие бы процессы в ней ни происходили. На поверхности проводника с током возникают дополнительные заряды, которые и создают постоянное электрическое поле внутри.

Обоснование появления зарядов на поверхности проводника с током следующее. Плотность тока внутри проводника по закону Ома пропорциональна напряженности поля:

$$\vec{j}=\lambda \vec{E}.$$

Возьмем дивергенцию обеих частей и воспользуемся первым уравнением Максвелла $$\text{div}\vec{E}=4\pi\rho$$ и законом сохранения электрического заряда в локальной форме $$\text{div}\vec{j}=-\partial\rho/\partial t$$:

$$-{\partial\rho\over\partial t}=4\pi\lambda\rho.$$(1)

Так как протекание тока — стационарный процесс, в котором величины со временем не меняются, то производная в левой части зануляется, поэтому правая часть — плотность зарядов внутри проводника — тоже есть 0. Следовательно, поле в проводнике может создаваться только зарядами на его поверхности.

Почему-то у этого простого обоснования есть противники, которые утверждают, что появление постоянного электрического поля вдоль проводника нельзя объяснить в классической электродинамике, и изобретают свои объяснения, например: источник тока создает избыток электронов с одного конца провода, и эти лишние электроны «расталкивают» другие электроны. Физического содержания в этих объяснениях нет, и мы не будем их рассматривать.

В этом посте попробуем найти, каким именно должно быть распределение поверхностного заряда, чтобы внутри проводника с постоянным сечением создалось однородное электрическое поле.

Близкая задача из электростатики

К сожалению, мы не можем найти точное распределение поверхностных зарядов по проводнику, если не учтем механизм того, как именно создается разность потенциалов на его концах. Вместо выбора такого механизма сделаем приближение, сказав что никакого механизма нет. Фактически, будем решать упрощенную задачу: как нужно распределить заряд по поверхности, чтобы поле внутри стало таким же, как и при стационарном протекании тока?

Разумеется, распределенный по поверхности проводника заряд без механизма создания разности потенциалов сразу же растечется (характерное время растекания можно найти из уравнения (1)), и, казалось бы, решать такую задачу бессмысленно. Но можно сформулировать задачу из электростатики о проводнике во внешнем однородном электрическом поле с точно таким же ответом:

Цилиндрический проводник длины l и радиуса R помещен во внешнее электрическое поле, так что его ось направлена по полю. Найти распределение поверхностных зарядов.

Действительно, в этом случае заряды так распределятся по поверхности проводника, что линейный потенциал внешнего поля $$\varphi_\text{внеш}=-|E|x$$ будет скомпенсирован их собственным потенциалом $$\varphi=kx$$ во всем объеме проводника.

Для полноты отметим, что аналогичная задача проводнике сферической формы имеет простое точное решение.

Наивный подход

$$ \newcommand{\drawCircle}[3]{ \draw (#1,#2) arc (90:270:#3 and #2); \draw[dashed] (#1,-#2) arc (-90:90:#3 and #2); } \newcommand{\drawTik}[2]{\draw (#1,0.1) -- ++ (0,-0.2) node[fill=white,below,inner sep=0,pos=1.4] {$#2$}} \begin{tikzpicture}[>=latex] \def\rx{4} \def\xx{-1.9} \def\x{1.9} \def\ry{1.2} \def\e{0.48} \node[above right,inner sep=2] at (0,\ry) {$R$} \node[below right,inner sep=2] at (0,-\ry) {$-R$} \node[below right] at (0,0) {$0$} \draw[->,very thin] (-\rx-1,0) -- (\rx+1,0) node[below] {$x$}; \draw[->,very thin] (0,-1.5*\ry) -- (0,2*\ry) node[left] {$r$}; \draw (\rx,0) ellipse (0.48 and \ry); \draw[] (-\rx,-\ry) -- (\rx,-\ry) (-\rx,\ry) -- (\rx,\ry); \drawCircle{-\rx}{\ry}{\e} \drawCircle{\xx-0.1}{\ry}{\e} \drawCircle{\xx+0.1}{\ry}{\e} \node[above] at (\xx,\ry) {$dx_1$} \drawTik{\xx}{x_1} \drawTik{\x}{x} \draw[dashed](\xx,\ry) -- (\x,0) \draw (\rx,0) ellipse (0.25 and 0.62); \draw (\rx,0) ellipse (0.3 and 0.75); \drawTik{-\rx}{-{l\over2}} \drawTik{\rx}{l\over2} \draw[dashed] (\x,0) -- (\rx,0.68) node[inner sep=2,pin={[pin distance=6, pin edge={<-,solid,black},fill=white,inner sep=1]30:$dr$}] {} \draw[->] (2.8,\ry+0.8) -- ++(2,0) node[pos=0.9,above] {$\vec{E}$}; \end{tikzpicture} $$

Обозначим плотность зарядов через $$\sigma_1(x)$$ на боковой поверхности и $$\sigma_2(r)$$ на поверхности оснований. Через эти величины можно выразить электрическое поле или потенциал внутри цилиндра, взяв интегралы по поверхности. Скажем, на оси цилиндра

$$\varphi(x)=\int\limits_{-l/2}^{l/2}{2\pi R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}+ \int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r) \over\sqrt{r^2+\left(x-{l\over2}\right)^2}} -\int\limits_{0}^{R}{2\pi r\,dr\,\sigma_2(r)\over\sqrt{r^2+\left(x+{l\over2}\right)^2}} =Ex.$$(2)

Здесь учтены симметрии задачи: вращательная симметрия вокруг оси повлияла на выбор элементов площади, а зеркальная симметрия выражается в том, что плотности зарядов на основаниях цилиндра имеют противоположный знак ($$\sigma_2$$ и $$-\sigma_2$$), и в том, что функция $$\sigma_1(x)$$ — нечетная.

Мы получили интегральное уравнение на $$\sigma_1(x)$$ и $$\sigma_2(r)$$. Я не смог решить его в явном виде. Можно было бы рассмотреть предельный режим, когда $$l\gg R$$, и поискать приближенное решение в области $$|x|\ll l$$. Тогда вкладом двух последних интегралов можно пренебречь, а в первом интегрировать от минус бесконечности до бесконечности:

$$\int\limits_{-\infty}^{\infty}{R\,dx_1\,\sigma_1(x_1)\over\sqrt{R^2+(x-x_1)^2}}=x.$$(3)

Здесь я опустил коэффициент пропорциональности, не влияющий на дальнейшие рассуждения. Это интегральное уравнение имеет вид свертки ядра $$k(x)=1/\sqrt{1+x^2/R^2}$$ и искомой функции. Такое уравнение можно решить, взяв преобразование Фурье от обеих частей:

$${\cal F}(\sigma_1)\int {e^{-ikx}\over\sqrt{1+\dfrac{x^2}{R^2}}}dx=\int xe^{-ikx}dx.$$

Интегрирование по частям справа дает $$\inline\int xe^{-ikx}dx=-i\delta(k)/k$$. Искомая функция ищется через обратное преобразование Фурье:

$$\sigma_1(x)={-i\over2\pi}\int\dfrac{\delta(k)e^{ikx} dk}{k\int {e^{-iks}\over\sqrt{1+\frac{s^2}{R^2}}}ds}.$$

Дельта-функция просто возвращает подынтегральное выражение при $$k=0$$. Интеграл в знаменателе можно выразить через модифицированную функцию Бесселя второго рода, и знаменатель стремится к 0 при $$k\to0$$. Получается, не существует «достаточно хорошей» функции $$\sigma_1(x)$$, определенной на всей вещественной оси, удовлетворяющей приближенному уравнению. Мы сделали слишком сильное упрощение, перейдя от уравнения (2) к уравнению (3).

Пока оставим попытки решить интегральное уравнение и посмотрим, что нам предлагает математика, а именно раздел, изучающий уравнения математической физики.

Аналитические методы заводят в тупик

Наша задача на языке математики формулируется так. Вне цилиндра потенциал подчиняется уравнению Лапласа $$\Delta\varphi=0$$ и стремится к нулю (как поле диполя) на бесконечности. На поверхности цилиндра потенциал фиксирован и описывается начальными условиями

$$\begin{align*}\varphi(x, R)&=Ex,\quad x\in\left[-{l\over2},{l\over2}\right],\\ \varphi\left(\pm{l\over2}, r\right)&=\pm E{l\over2},\quad r\in\left[0,R].\end{align*}$$

Это формулировка задачи Дирихле для уравнения Лапласа. Решение у этой задачи существует и оно единственно. Потенциал определяет электрическое поле вне цилиндра, а скачок нормальной составляющей электрического поля на границе цилиндра пропорционален искомой поверхностной плотности заряда.

Уравнение Лапласа в цилиндрических координатах с учетом цилиндрической симметрии задачи записывается так:

$${1\over r}{\partial\over\partial r}\left(r{\partial\varphi\over\partial r}\right)+{\partial^2\varphi\over\partial x^2}=0.$$(4)

Стандартный метод решения таких уравнений — метод разделения переменных, он же метод Фурье. Искомая функция ищется в виде суммы (конечной, счетной или интеграла) произведений функций, в которых каждый сомножитель зависит только от своей переменной:

$$\varphi(x,r)=\sum_kX_k(x)R_k(r).$$

Мы хотим, чтобы (4) выполнялось не только для всей суммы целиком, но и для каждого элемента $$X_k(x)R_k(r)$$. Подставляем его в (4) и получаем:

$${1\over rR_k}{\partial\over\partial r}(rR_k')=-{1\over X_k}X_k''=-\lambda_k.$$

После такой подстановки получилось представить равенство так, что левая его часть зависит только от координаты r, а правая — только от координаты x. Равенство возможно, только если никакой зависимости нет, то есть и правая, и левая часть равны некоторой константе $$\lambda_k$$. Дальше, в зависимости от вида граничных условий, выбирается одно из двух получившихся дифференциальных уравнений

$$\left\{ \begin{array}{l} R_k'+rR_k''+\lambda_krR_k=0,\\ X_k''-\lambda_kX_k=0,\end{array} $$

и исследуется задача Штурма — Лиувилля: при каких $$\lambda_k$$ с учетом граничных условий у этого дифференциального уравнения возможны решения. Наконец, для этих $$\lambda_k$$ решается оставшееся дифференциальное уравнение и ответ обычно записывается в виде ряда по собственным функциям оператора Штурма — Лиувилля.

Проделать эту процедуру в нашем случае не представляется возможным. Дело в том, что первое уравнение нужно решать на области $$r\in[R,\infty)$$, когда $$x\in\left[-{l/2},{l/2}\right]$$, и на области $$r\in[0,\infty)$$ в противоположном случае. Аналогично со вторым уравнением. Представить решение по всему пространству вне цилиндра в виде одного ряда по собственным функциям какой-либо задачи Штурма — Лиувилля не получается. Есть предложение разбить пространство на несколько частей (как минимум на 3, а то и на 5), решить задачу Дирихле в каждой из них, а затем сшивать эти решения вместе с производными, накладывая дополнительные условия на коэффициенты в рядах и выкидывая слагаемые, которые сшить нельзя. Я не стал заходить в эти дебри, тем более что ответ в виде непонятного ряда по функциям Бесселя вряд ли вызовет известное ощущение завершенности от решения задачи.

Численное решение

Возвращаемся к интегральному уравнению (2) из наивного подхода. Зададимся какими-нибудь конкретными значениями размеров. Пусть длина провода будет 10 сантиметров, а его диаметр — 1 миллиметр. В подходящих единицах измерения можно считать, что $$l=2$$, $$R=0,\!01$$, а коэффициент пропорциональности в уравнении (2) отсутствует. Таким образом, мы будем решать уравнение

$$\int\limits_{-1}^{1}{dx_1\,\sigma_1(x_1)\over\sqrt{1+10000(x-x_1)^2}}+ \int\limits_{0}^{0,01}r\,dr\,\sigma_2(r)\left({1 \over\sqrt{r^2+\left(x-1\right)^2}} -{1\over\sqrt{r^2+\left(x+1\right)^2}}\right) =x.$$

Приближение к его решению можно искать не на всех функциях, а на определенном классе функций, например, на нескольких первых слагаемых разложения в степенной ряд. Отклонение получающейся функции $$\widetilde{\varphi}_a(x)$$ от правой части будем оценивать как интеграл от квадрата разности, и будем подбирать параметры функций a, добиваясь минимума этого интеграла:

$$f(a)=\int\limits_{-1}^{1}\left(\widetilde{\varphi}_a(x)-x\right)^2dx\to \text{min}.$$

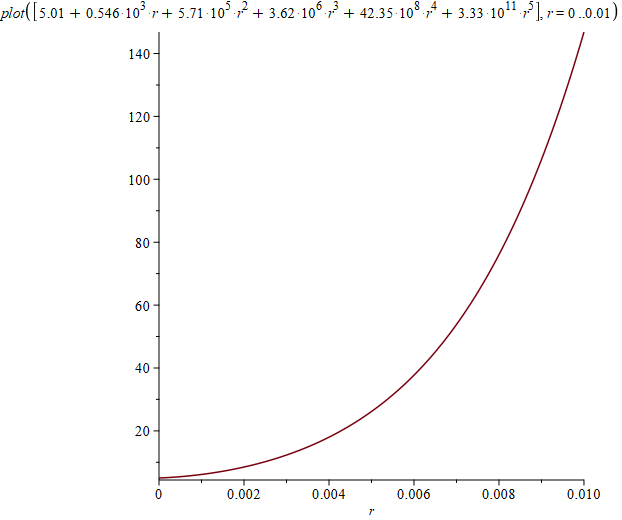
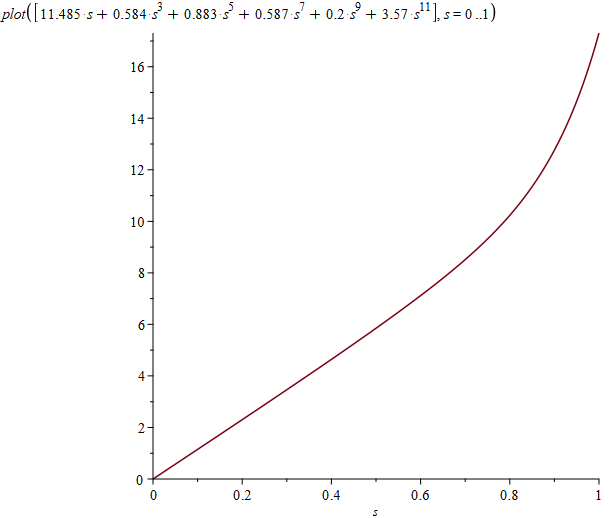
Как обычно, решение попробовал найти в Maple. У меня не получилось заставить его минимизировать такой интеграл, зависящий от набора параметров. Поэтому я оставлял только один параметр, заменяя остальные их текущими значениями, строил график по этому параметру и определял его текущее значение в минимуме. Фактически выполнял вручную итерации из метода координатного спуска для функции $$f(a)$$ такого типа:

f := a -> int((
   int((11.485*s + 0.584*s^3 + 0.883*s^5 + 0.587*s^7 + 0.2*s^9 + 3.57*s^11)/
      sqrt(1 + 10000*(x - s)^2), s = -1 .. 1, numeric) +
   int((5.01 + 5.46*10^2*r + 5.71*10^5*r^2 + 3.62*10^6*r^3 + 42.35*10^8*r^4 + a*r^5)*
      r*(1/sqrt(r^2 + (1 - x)^2) - 1/sqrt(r^2 + (x + 1)^2)), r = 0 .. 0.01, numeric)
- x)^2, x = -1 .. 1, numeric)

Здесь все интегралы отмечены как «numeric», чтобы Maple не пытался вычислить их аналитически. В моем случае попытка аналитического вычисления существенно замедляла работу, так что я не мог дождаться результата. Потенциал на оси для моего приближения на глаз отличается от прямой только у краев:

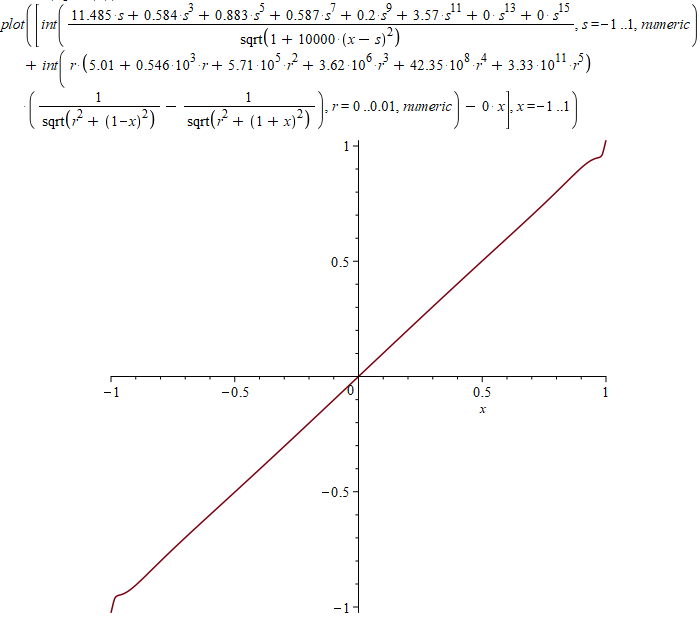
График отклонения от прямой (интеграл от квадрата этой функции я минимизировал, здесь масштаб по осям разный):

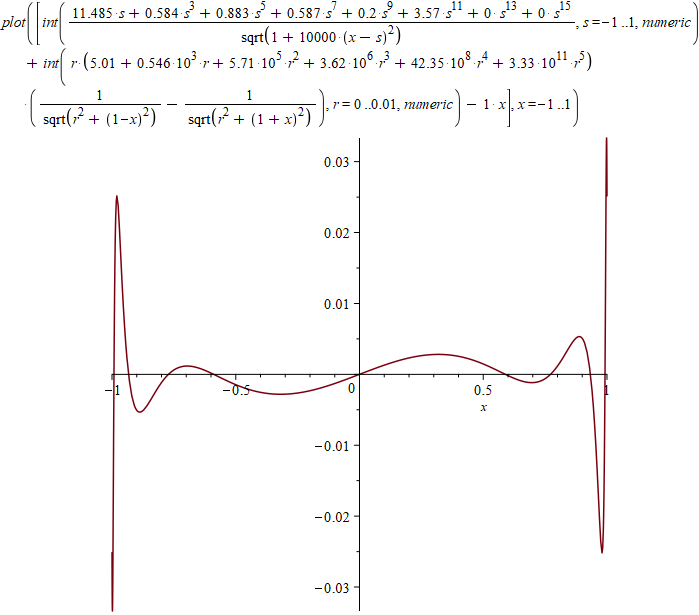
Можно также нарисовать графики плотностей на основаниях и на боковой поверхности:

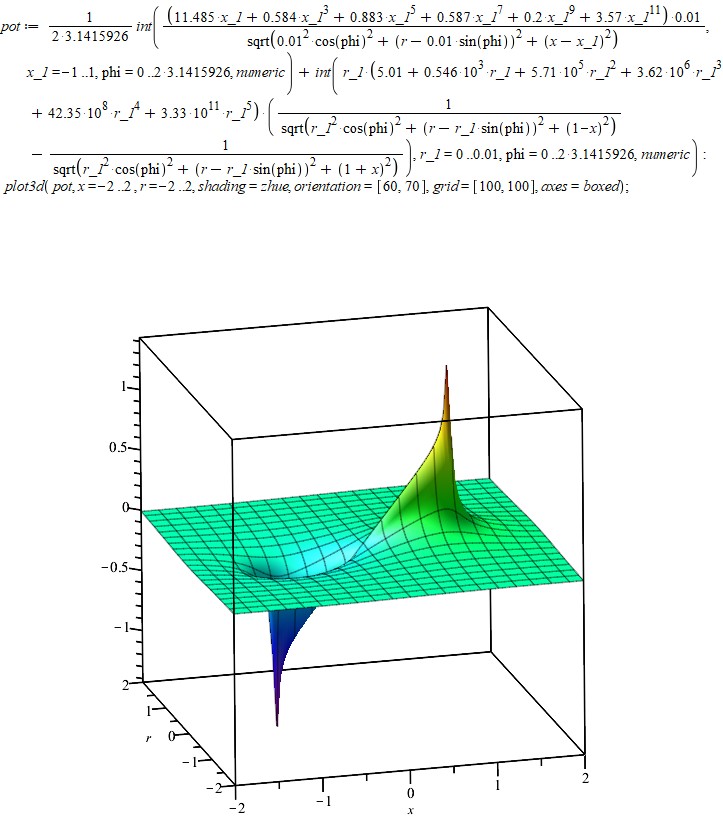
Перейдем теперь к исследованию этого решения по всему пространству. Чтобы найти потенциал в произвольной точке не на оси, нужно добавить интегрирование по углу, так как теперь расстояние от элемента поверхности до расчетной точки уже зависит от угла. Трехмерный график потенциала выглядит так:

Нарисуем сечения эквипотенциальных поверхностей:

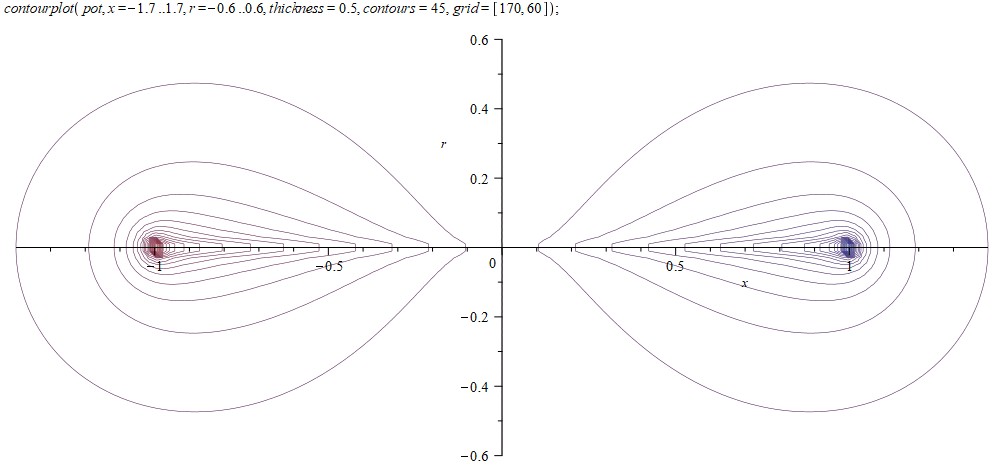
Рассмотрим поближе край проводника:

На полученный потенциал можно наложить внешнее электрическое поле и проверить, какая будет поверхность нулевого потенциала. Для правильного решения она должна совпадать с цилиндрической поверхностью проводника. В нашем случае у его краев (от 0,7 до 1) наблюдаются заметные утолщения, наглядно показывающие степень полученного приближения:

Вывод

Мы пытались решить две близких задачи: одна об электрическом поле внутри и снаружи провода с током, вторая о разделении зарядов в проводнике во внешнем электрическом поле. Аналитические методы не привели к успеху. Пришлось искать приближенное численное решение в Maple и использовать встроенные инструменты визуализации решения.

Из этого мини-исследования на третьем курсе получилась бы хорошая курсовая работа. Преподаватели урматов и вычматов были бы довольны.

Брахистохрона под землей

Мотивация

В сборниках задач по физике часто встречается известная задача о продолжительности свободного падения тела сквозь прямой тоннель, проходящий через центр Земли и соединяющий диаметрально противоположные точки. Для решения нужно знать, что сила притяжения к центру Земли в таком тоннеле уменьшается линейно до нуля, и тело, упавшее в такой тоннель, будет совершать гармонические колебания. Время движения составляет половину периода и для модели однородной Земли равно 42 минуты. Более того, это время не меняется для любого прямого тоннеля, идущего по хорде (не проходящего через центр), если трением можно пренебречь.

Также в научно-популярных книгах и других источниках встречается красивая задача о брахистохроне — кривой скорейшего спуска. В ней требуется найти форму желоба, проложенного между двумя фиксированными точками A и B, чтобы время скатывания тела из A в B было наименьшим. В однородном гравитационном поле брахистохроной является дуга циклоиды.

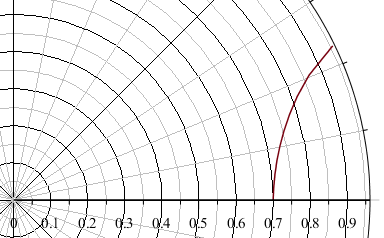
Вполне естественным кажется желание скрестить эти две задачи и выяснить, какой формы нужно проложить тоннель под землей, чтобы в идеальной ситуации без трения между точками A и B на поверхности (скажем, между двумя городами) поезд проезжал за наименьшее время. Эта новая задача имеет аналитическое решение. Её ответом является гипоциклоида — кривая, которую описывают точки окружности радиуса $$a$$, катящейся без проскальзывания внутри другой окружности радиуса $$b$$. Вот как записывается параметрическое уравнение гипоциклоиды и выглядит ее чертеж:

$$\begin{cases} x=(b-a)\cos\theta+a\cos\dfrac{b-a}{a}\theta,\\ y=(b-a)\sin\theta-a\sin\dfrac{b-a}{a}\theta. \end{cases}$$

$$\begin{tikzpicture} \def\clr{black} \def\a{1} \def\b{5} \newcommand{\xt}[1]{(\b-\a)*cos(#1)+\a*cos((\b-\a)*#1/\a} \newcommand{\yt}[1]{(\b-\a)*sin(#1)-\a*sin((\b-\a)*#1/\a} \draw[cyan,very thin] (-\b-1,-\b-1) grid (\b+1,\b+1); \draw[->] (-\b-1,0) -- (\b+1,0); \draw[->] (0,-\b-1) -- (0,\b+1); \draw[\clr,thick] (0,0) circle (\b); \draw[\clr,dashed,very thin] (0,0) circle (\b-\a); \draw[line width=2pt,orange!80!red] plot[samples=60,domain=0:\a*360,smooth,variable=\t] ({\xt{\t}},{\yt{\t}}); \def\t0{40} \draw[\clr!50!black] (\t0:\b-\a) circle (\a); \draw[purple,fill] ({\xt{\t0}},{\yt{\t0}}) circle (2pt) -- (\t0:\b-\a) circle (1pt) node [midway, sloped, above] {\scriptsize $a$} -- (0,0) circle (1pt) node [midway, sloped, above] {\scriptsize $b-a$} node [below right] {$O$}; \node[\clr,fill=white,text width=1cm,align=center] at (-\b,\b) {$a=\a$ $b=\b$}; \end{tikzpicture}$$

Я задумался об этой задаче в старших классах или на первом курсе института, но тогда, разумеется, у меня не хватало знаний для решения в аналитическом виде. Я вернулся к задаче на четвертом курсе и смог довести вычисления до конца, не обращаясь к источникам, но и не без помощи Maple. Эти вычисления были одними из самых сложных среди всех задач с явным аналитическим ответом, которые я решал.

Физическая сторона задачи

$$\begin{tikzpicture} \def\a{1} \def\b{5} \draw ([shift=(-10:\b)]0) arc (-10:90:\b); \draw[-stealth] (\b,0) node[right]{$A$} -- node[pos=0.92,above,inner sep=2] {$\varphi$} (0,0) -- (\b*0.35,\b*0.6) node[below,pos=0.9]{$\vec{r}$} ; \node[above] at (\b*0.32,\b*0.95) {$B$}; \draw[line width=1pt,orange!80!red] plot[samples=12,domain=0:72,smooth,variable=\t] ({(\b-\a)*cos(\t)+\a*cos((\b-\a)*\t/\a},{(\b-\a)*sin(\t)-\a*sin((\b-\a)*\t/\a}); \end{tikzpicture}$$

Движение поезда по подземному тоннелю будем рассматривать в полярных координатах. Считаем потенциал внутри Земли осцилляторным: $$U\sim r^2$$. Запишем закон сохранения энергии с учетом нулевой скорости поезда на поверхности:

$${mv^2\over 2}+{m\omega^2r^2\over 2}={m\omega^2r_0^2\over 2},$$(1)

где $$r_0$$ — радиус Земли, $$\omega=2\pi/T$$ — круговая частота колебаний, соответствующая периоду в 84 минуты. Время движения через тоннель $$\inline t=\int{dl\over v}$$. Выражаем скорость $$\inline v=\omega\sqrt{r_0^2-r^2}$$ из (1) и для времени движения поезда через тоннель получаем следующее выражение:

$$t=\int{dl\over v}={1\over\omega}\int{\sqrt{dr^2+r^2d\varphi^2}\over\sqrt{r_0^2-r^2}}={1\over\omega}\int{\sqrt{r'^2+r^2}\over\sqrt{r_0^2-r^2}}d\varphi,$$

Здесь мы выразили элемент длины пути через полярные координаты. Таким образом, задача свелась к поиску функции $$r(\varphi)$$ с фиксированным значением $$r(\varphi_A)=r(\varphi_B)=r_0$$ на концах отрезка, для которой функционал

$$\omega t=\int\limits_{\varphi_A}^{\varphi_B}\sqrt{{r'^2+r^2}\over{r_0^2-r^2}}d\varphi$$(2)

принимает наименьшее значение.

Математическая сторона задачи

Задача по минимизации интеграла (2) на множестве достаточно хороших с точки зрения физика функций (скажем, дифференцируемых сколько нужно раз) — типовая задача вариационного исчисления. Заметим, что подынтегральное выражение в (2) можно представить в виде функциональной зависимости от $$r$$ и ее производной:

$${\cal L}(r,r')=\sqrt{{r' ^2+r^2}\over{r_0^2-r^2}}$$(3)

Из курса дифференциальных уравнений известно, что экстремальные значения (2) нужно искать на решениях дифференциального уравнения Эйлера — Лагранжа:

$${\partial{\cal L}\over\partial r}-{d\over d\varphi}{\partial{\cal L}\over\partial r'}=0.$$

Если вы вооружитесь бумагой и ручкой и попробуете подставить сюда (3), то быстро заметите сложность получившегося дифференциального уравнения со второй производной и нагромождением корней и осознаете тупиковость этого подхода. В системах компьютерной алгебры есть встроенные пакеты для решения вариационных задач. Вот пример для Maple, где вы видите трехэтажное дифференциальное уравнение:

Кроме того, Maple заботливо подсказывает, что у получившегося дифференциального уравнения есть первый интеграл. И тут вы вспоминаете, что на курсах теоретической механики и дифференциальных уравнений всё-таки рассказывают некоторые полезные вещи. В частности, у уравнений Эйлера — Лагранжа есть интегралы движения. В нашем случае интеграл движения имеет вид

$${\cal L}-r'{\partial{\cal L}\over\partial r'}=const.$$

Если вам проще воспринимать физику, а не математику, вы можете представить некоторую систему, описываемую функцией Лагранжа (3). Движение во «времени» $$\varphi$$ от «момента» $$\varphi_A$$ к $$\varphi_B$$ будет происходить по такой траектории $$r(\varphi)$$, на которой «действие» (2) примет экстремальное значение. Так как функция Лагранжа $$\cal L$$ не зависит от «времени» $$\varphi$$, то у системы есть сохраняющаяся величина — «энергия». Первый интеграл выше как раз и дает величину этой «энергии».

Выполним дифференцирование:

$$k={\cal L}-r'{\partial{\cal L}\over\partial r'}=\sqrt{{r' ^2+r^2}\over{r_0^2-r^2}} -r'{r'\over\sqrt{r_0^2-r^2}\sqrt{r'^2+r^2}}={r^2\over\sqrt{r_0^2-r^2}\sqrt{r'^2+r^2}}.$$

Мы пришли к дифференциальному уравнению первого порядка $$\inline r^2=k\sqrt{r'^2+r^2}\sqrt{r_0^2-r^2}$$, в котором разделяются переменные и получается следующий интеграл:

$$\varphi=\int{dr\over\sqrt{\cfrac{r^4}{k^2(r_0^2-r^2)}-r^2}}.$$

Его можно вычислить аналитически. Например, Maple выдает такой результат:

Чтобы доказать, что это выражение описывает гипоциклоиду, нужно взять её параметрическое уравнение и проделать достаточно громоздкие преобразования обратных тригонометрических функций, которые я не буду сейчас приводить.

В интернете опять кто-то неправ, или учимся избегать ошибок

Когда я занимался этой задачей, мне попадалась статья с нестандартными вычислениями: вместо полярных координат использовались декартовы. Тогда мне показалось, что автору очень повезло: уравнение гипоциклоиды в параметрической форме написано в таком виде, что параметр оказался пропорциональным физическому времени. При подготовке этой заметки я опять наткнулся на ту же статью. Сейчас эти нестандартные вычисления кажутся мне ошибочными.

Я предположил, что это чья-то студенческая работа с не очень высокими требованиями. Решил подробнее узнать об авторе, Аманде Максхэм, и нашел заметку в ее блоге как раз об этой статье. Она пишет, что эта статья выдается на первой странице в гугле по запросу «gravity train». Раз так, то тем более нужно разобраться, скрывается ли за нестандартными вычислениями какой-то хитрый прием, или это просто ошибка. Причем моя цель не в том, чтобы показать, что в интернете опять кто-то неправ, а в том, чтобы научиться отличать правильный способ рассуждения от неправильного.

Вот ключевой момент статьи, в котором делается попытка доказать, что гипоциклоида — искомое решение:

Вопросы начинаются с формулы (19), в которой пропущен дифференциал, и поэтому не совсем понятно, по какому параметру дальше берутся производные. Эти же производные сохраняются вплоть до (22), куда подставляются $$x(t)$$ и $$y(t)$$ из (24) и (25). Но параметр $$t$$ в (24) и (25) не может быть временем $$t_\text{физ}$$, так как он является аргументом тригонометрических функций и должен быть безразмерным. Получается, это некоторый параметр, задающий положение точки на траектории, но не являющийся временем.

(Попутно возникает мини-вопрос о том, откуда взялась разность $$x'^2-y'^2$$ вместо соответствующей суммы в правых частях (20) и (21), но эта опечатка в четырех местах не распространяется на дальнейшие рассуждения, и мы к ней придираться не будем.)

Еще возникает вопрос о степенях свободы. В уравнениях (19) и (22) неизвестные величины — $$(x, y, t)$$. Таким образом, эти уравнения содержат лишнюю степень свободы по сравнению с неизвестными $$(r, \varphi)$$ из нашего рассмотрения (и из предыдущего раздела работы Аманды). Эта избыточность мешает корректному применению формализма Лагранжа — Эйлера. Какие признаки этого мы видим?

1. (22) — не единственное возможное следствие из (20) и (21). Если поделить (20) на (21), получим, что $$(y'/x')^2=(dy/dx)^2=const$$, а это есть уравнение, описывающее не гипоциклоиду, а прямую траекторию. Почему это следствие из (20) и (21) менее правильное, чем (22)?

2. (22) с точностью до константы $$C$$ по форме совпадает с законом сохранения энергии, с которого начиналось решение. Действительно, выражение в левой части напоминает квадрат скорости, а в правой — разницу квадратичных потенциалов, то есть изменение потенциальной энергии. Присутствие константы $$C$$ объясняется тем, что производные в (22) берутся не по физическому времени $$t_\text{физ}$$, а по другому параметру $$t$$, который в $$C$$ раз меньше: $$t_\text{физ}=Ct$$. Если бы связь $$t_\text{физ}=Ct$$ нарушилась, то (22) противоречило бы закону сохранения энергии. Таким образом, (22) можно получить без применения лагранжева формализма, просто напрямую из закона сохранения энергии с помощью замены $$t_\text{физ}=Ct$$. Следовательно, (22) не может иметь большего физического содержания, чем закон сохранения энергии, и не несет информацию о траектории, минимизирующей время.

3. (24) и (25) формально являются решением (22), так как зануляют его при выполнении (26). Но они не являются единственным решением. Фактически, любое физически возможное движение из-за сохранения энергии будет удовлетворять уравнению (22). Важно лишь выбрать параметризацию этого движения так, чтобы физическое время было пропорционально параметру. Возьмем для примера движение по хорде $$x(t)=A$$, $$y(t)=B\cos t$$, где $$\inline A^2+B^2=R^2$$, подставим в (22) и при должном выборе константы $$C$$ (то есть при выборе правильного движения во времени вдоль хорды) получим тождество:

$$RB^2\sin^2 t=gC^2(R^2-A^2-B^2\cos^2 t)=gC^2B^2\sin^2 t.$$

Таким образом, осцилляторное движение по тоннелю в виде прямой хорды также является решением (22). Но оно отнюдь не минимизирует функционал (19) для общего времени движения между двумя точками.

Я так и не смог понять, можно ли провести рассуждения в декартовых координатах с избыточной степенью свободы и получить правильный ответ. Понятно желание использовать декартовы координаты, а не полярные, так как в них уравнение гипоциклоиды выглядит проще. Но интуитивно кажется, что лишняя степень свободы, появившаяся в функционале времени и соответствующая выбору закона движения тела вдоль траектории, не дает при применении лагранжева формализма достаточных ограничений на траекторию.

Я оставил комментарий в блоге Аманды с вопросами. Но никакой реакции не последовало.

Напишите свой комментарий, если видите ошибку в моих рассуждениях, или если знаете, как сделать корректное рассмотрение в декартовых координатах.

Добавлено 13.10.2023: я нашел у себя в архиве файлов сохраненную в 2008 году статью о брахистохроне, и это не работа Аманды. Автор не указан, статья располагалась по этой ссылке. Ход решения в этих статьях одинаков, но видно, что написаны они по-разному, и, похоже, разными авторами. «Опечаток» в этой статье меньше, но иногда дифференциал под интегралом тоже пропадает. Разумеется, критика идеи решения относится в равной мере и к этой статье.

туда →